Generating Sentences from a Continuous Space
連続空間からのテキスト生成
Generating Sentences from a Continuous Space
author: Samuel R. Bowman, Luke Vilnis, Oriol Vinyals, Andrew M. Dai, Rafal Jozefowicz & Samy Bengio
1. はじめに
リカレントニューラルネットワーク言語モデル (RNNLMs, Mikolov et al., 2011) は,自然言語文の教師なし生成モデリングにおける最先端の技術を代表するものである。 教師ありの設定では,課題固有の特徴を条件とする RNNLM 復号化器は,機械翻訳 (Sutskever ら,2014; Bahdanau ら,2015) および画像脚注付け (Vinyals ら,2015; Mao ら,2015; Donahue ら,2015) などの課題の最先端技術である。 RNNLM は進化する分散状態表現に基づいて単語単位で文を生成するため,有意な独立性の仮定を持たない確率的モデルとなり,長期依存性を含む系列上の複雑な分布をモデル化することが可能である。 しかし RNNLM はモデル構造を一連の次段階予測に分解することで,話題などの大域的特徴や高次構文特性の解釈可能な表現を顕に示さない。
i store to buy some groceries .
i were to buy any groceries .
horses are to buy any groceries .
horses are to buy any animal .
horses the favorite any animal .
horses the favorite favorite animal .
horses are my favorite animal .
表 1: 従来の自己符号化器で 2 文の符号化の中間点から貪欲に復号して生成された文。 中間文は,もっともらしい英語ではない。
我々は,このような大域特徴を連続潜在変数に明示的に取り込むように設計された RNNLM の拡張を提案する。 直感的には,このようなモデルにおける最尤法学習は,難解な推論問題を呈する。 画像のモデリング (Gregor et al.,2015),手書き,及び自然音声 (Chung et al.,2015) における最近の成功からインスピレーションを得て,我々のモデルは変分自己符号化器のアーキテクチャを用いてこれらの困難を回避し,変分推論の最近の進歩 (Kingma and Welling,2015; Rezende et al.,2014) を利用して,潜在変数を持つ強力なニューラルネットワーク生成モデルのための実践的学習技術を導入している。
我々の貢献は以下の通りである。 テキストのための変分自己符号化器アーキテクチャを提案し,それを訓練する際の障害と我々の提案する解決策を議論する。 グローバル変数が明示的に必要とされない標準的な言語モデリング評価において,このモデルは既存のRNNLMs と同等の性能をもたらすことを見出した。 また,より大規模なコーパスを用いて,欠損単語を埋め込む課題で我々のモデルを評価した。 この課題では,ノンパラメトリック 2 標本検定と敵対的学習からヒントを得て,難解な尤度計算の問題を回避し,敵対的分類器を用いた新しい評価戦略を導入している。 この設定において,我々のモデルは大域的潜在変数により,より単純なモデルが失敗するところでもうまくやることができる。 最後に,我々のモデルが文の高次特徴を学習する能力を分析するためのいくつかの定性的な技法を紹介する。 我々は,純粋に決定論的な復号化によって多様で一貫性のある文を生成できること,そして文と文の間を滑らかに補間できることを見出した。
2. 背景
2.1 教師なし文符号化
標準的な RNN 言語モデルは,前の単語と進展する隠れ状態を条件として,文の各単語を予測する。 このモデルは効果的ではあるが,文全体のベクトル表現を学習しない。 連続的な潜在的文表現を取り入れるためには,まず,文と分散表現の間の写像を行う方法が必要であり,教師なし設定で学習することが可能である。 この問題に対して強力な生成モデルは存在しないが,3 つの非生成技術が有望視されている: 系列自己符号化器,スキップソート,段落ベクトルである。
系列自己符号化器は,教師あり下流課題の系列モデルの事前学習 (Dai and Le, 2015) や完全な文書の生成(Li et al.,2015a) において成功を収めている。 自己符号化器は,符号化関数 enc と確率的復号化モデル $p(x\vert z=\varphi_{\text{enc}}(x))$ からなり,$x$ の学習コードである $z$ を条件とした例 $x$ の尤度を最大化させるものである。 系列自己符号化器の場合,符号化器と復号化器はともに rnn であり,事例はトークン列である。
標準的な自己符号化器は,大域的な意味的特徴を抽出するのに有効でない。 表 1 では,2 つの文に対する符号化間のパスまたはホモトピーを計算し,それぞれの中間符号を復号化した結果を示している。 中間文は一般に非文法的であり,一方から他方へスムーズに遷移することはない。 このことは,これらのモデルが一般に文の符号化のための滑らかで解釈可能な特徴系を学習していないことを示唆している。 さらに,これらのモデルは $z$ に関する事前分布を組み込んでいないため,文に確率を割り当てたり,新しい文をサンプリングするために使用することはできない。
他の 2 つのモデルは文の符号化学習に有望であるが,生成的な設定では使用することができない。 スキップソートモデル (Kiros et al.2015) は,系列自己符号化器と同じモデル構造をとる教師なし学習モデルであるが,ターゲット文そのものではなく,ターゲット文から隣接する文を条件としたテキストを生成するものである。 最後に,段落ベクトルモデル (Le and Mikolov, 2014) は,非再帰型文表現モデルである。 段落ベクトルモデルでは,文の単語を予測するためにそれを使用することを目的として,見込み符号化ベクトルに対して勾配に基づく推論を行うことにより,文の符号化が得られる。
2.2 変分自己符号化器
変分自己符号化器 (VAE, Kingma and Welling, 2015; Rezende et al.,2014) は,標準自己符号化器の正則化バージョンに基づく生成モデルである。 このモデルは,コード上の規則的な形状を強制する隠れコード $z$ に事前分布を課し,祖先 (前向き) サンプリングを用いてモデルから適切なサンプルを抽出することを可能にする。
VAE は決定論的関数 $\varphi_{\text{enc}}$ を学習された事後確率認識モデル $q(z\vert x)$ で置き換えることにより,自己符号化器アーキテクチャを変更する。 このモデルは $z$ に関する近似的な事後分布 (通常は対角ガウス分布)を,$x$ で条件づけられたニューラルネットワークでパラメタライズする。 直感的には VAE はコードを単一点としてではなく,潜在空間における柔らかい楕円形の領域として学習し,孤立したコードとして学習データを記憶するのではなく,コードが空間を埋めるように強制的に学習させる。
もし VAE が標準自己符号化器の再構成目的で学習された場合,$q(z\vert x)$ の分散を消滅的に小さくすることで入力を決定論的に符号化するよう学習するだろう (Raiko et al.,2015)。 その代わりに VAE は,その事後分布を事前分布 $p(z$, 一般に標準ガウス分布 ($\mu=0,\sigma=1$) に近づけるようモデルに促す目的関数を使用する。 さらに,この目的関数はデータの真の対数尤度に対する有効な下界であり,VAE は生成モデルであると言える。 この目的関す次のような形式をとる:
\[\mathcal{L}(\theta, x)= - D_{KL} \left[q_ {\theta}(z\vert x)\vert\vert p(z) \right] + \mathbb{E}_ {q_ {\theta}(z\vert x)}\left[\log p_ {\theta}(x\vert z)\right] \le \log p(x) \tag{1}\]このため,モデルは事前分布の下で妥当な確率を持つ潜在空間のあらゆる点から,もっともらしい文を解読できるようになることを強制される。 以下に示す VAE モデルを用いた実験では,Kingma and Welling (2015) のガウス再パラメータ化トリックを用いて,事前・事後分布 $p(z)$ と $q(z|x)$ に対角ガウス分布を用いる。 我々は,確率的勾配降下でモデルを訓練し,各勾配段階で $q(z\vert x)$ からの単一のサンプルを使用して再構成コストを推定するが,再び Kingma and Welling (2015) に従って,閉形式のコスト関数の KL ダイバージェンス項を計算する。
3. 文章のための VAE
我々は,符号化器と復号化器に単層の LSTM RNNs (Hochreiter and Schmidhuber, 1997) を用いて,変分自己符号化器をテキストに適応させ,ガウス事前分布を隠れコードに対する正則化として作用させた系列自己符号化器を本質的に形成している。 復号化器はこの隠れコードに条件付けられた特別な RNN 言語モデルとして機能し,隠れコードが有用な情報を含まない縮退した設定では,このモデルは実質的に RNNLM と等価となる。 このモデルは 図 1 に示すように,後述するすべての実験に用いられている。
このアーキテクチャの変種として,時間ステップ毎にサンプリングした $z$ を復号化入力に連結する,分散にソフトプラスのパラメトリゼーションを用いる,復号化と潜在変数,符号化器と潜在変数間に深層フィードフォワードネットワークを用いる,などを検討した。 これら変種を用いた場合,モデルの性能にはほとんど差がないことがわかった。 しかし,符号化器と復号化器の間にフィードフォワードネットワークを含む場合,モデルが学習するために高速ネットワーク層を使用する必要があることが分かった (Srivastava et al.2015)。 ハイパーパラメータのチューニングについては,付録で説明する。
我々はまた DRAW (Gregor et al.,2015) に倣った多段階サンプリングモデルや,正規化フローを用いた事後近似 (Rezende and Mohamed, 2015) など,より高度な認識モデル $q(z\vert x)$ の実験も行った。 しかし,我々はプレーンな VAE から有意な利得を得ることができなかった。
これまで VAEs の最も強力な成果は,画像のような連続的な領域に対するものであったが,離散的な系列に対する研究も行われている。 我々のモデルと同じ高レベルのアーキテクチャを共有する RNN 符号化器と復号化器を使用してこれを行うための技法は,Fabius and van Amersfoort (2014) で音楽のモデリングのための 変分リカレント自己符号化器(VRAE) の名前で提案された。 音声,手書き,l音楽のモデリングのための RNN スタイルのモデルに連続的な潜在変数を含める研究は他にもあるが (Bayer and Osendorfer,2015; Chung et al.,2015) ,これらのモデルはタイムステップごとに個別の潜在変数を含み,大域特徴をモデル化する我々の目標には不向きであった。
我々と似た目標を持つ最近の論文では Miaoら(2015) が,テキストを系列としてではなく,単語の袋としてモデル化する効果的な VAE ベースの文書レベル言語モデルを紹介している。 彼らは,ネットワークの符号化器と復号化器の部分を同時ではなく交互に学習させる必要があることを簡潔に述べており,おそらく 3.1 節で議論した問題のいくつかに対処する方法として,このことを述べている。
3.1 最適化の課題
我々のモデルは文の内容に関する大域的な潜在的表現を学習することを目的としている。 変分下界の目的関数 式(1) を見ることで,我々のモデルが大域的特徴を学習する度合いを定量化することができる。 この下界は 2 つの項に分かれる。 すなわち (交差エントロピーとして表現される) 事後確率の下でのデータ尤度と,事前確率からの事後確率への KL ダイバージェンスである。 潜在変数 $z$ に有用な情報を持つモデルは,非ゼロの KL ダイバージェンス項と比較的小さな交差エントロピー項を持つことになる。 ごく稀なケースを除き,ほとんどのハイパーパラメータを用いた学習では $q(z\vert x)$ を事前分布 $p(z)$ に等しく設定し,コスト関数の KL ダイバージェンス項をゼロにするモデルを一貫して生成する。
このような場合,モデルは本質的に RNNLM として振る舞う。 このため,出力文に対する任意の分布を表現することができ (厄介な左・右因数分解を伴う可能性はあるが),それによって最適に近い尤度を達成することができる。 画像モデリングのための VAEs に関する以前の仕事 (Kingma and Welling, 2015) は,より弱い独立画素復号化器モデル $p(x\vert z)$ を用い,良い尤度を達成するためにモデルが大域的潜在変数を使用せざるを得なくなった。 関連する結果として LSTM 復号化器を使用する画像生成への最近のアプローチは VAE スタイルの大域的潜在変数なしでうまくいくこと (Theis and Bethge, 2015)。
学習におけるこの問題のある傾向は,事後サンプリング過程によってもたらされるような,隠れ状態の微妙な変動に対する LSTM 復号化器の感度によって,さらに悪化する。 これにより,モデルは当初 $z$ を無視し,より簡単に最適化された復号化器でデータを説明し,低いぶら下がりの果実を狙うことを学習する。 一旦これが起こると,復号化器は符号化器を無視し,両者の間を勾配信号がほとんど通らなくなり,KL コスト項がゼロとなる望ましくない安定均衡をもたらす。 我々はこの問題を軽減するために 2 つの技術を提案する。
3.3.1 KL コスト焼きなまし
この問題に対する簡単なアプローチでは,学習時にコスト関数の KL 項に可変の重みを加える。 学習開始時には,その重みをゼロに設定し,モデルができるだけ多くの情報を $z$ に符号化するよう学習する。 そして,学習が進むにつれて,この重みを徐々に増加させ,モデルに符号化を平滑化させ,事前分布に詰め込ませる。 この重みは 1 になるまで増加させ,その時点で重み付きコスト関数は真の変分下界と等価になる。 この設定では,学習の初期段階では学習データ尤度の適切な下界を最適化しないが,それでも収束時にはその下界の値が改善されることが分かる。 これは,バニラ自己符号化器 から VAE へのアニーリングと考えることができる。 この増加の割合はハイパーパラメータとして調整される。
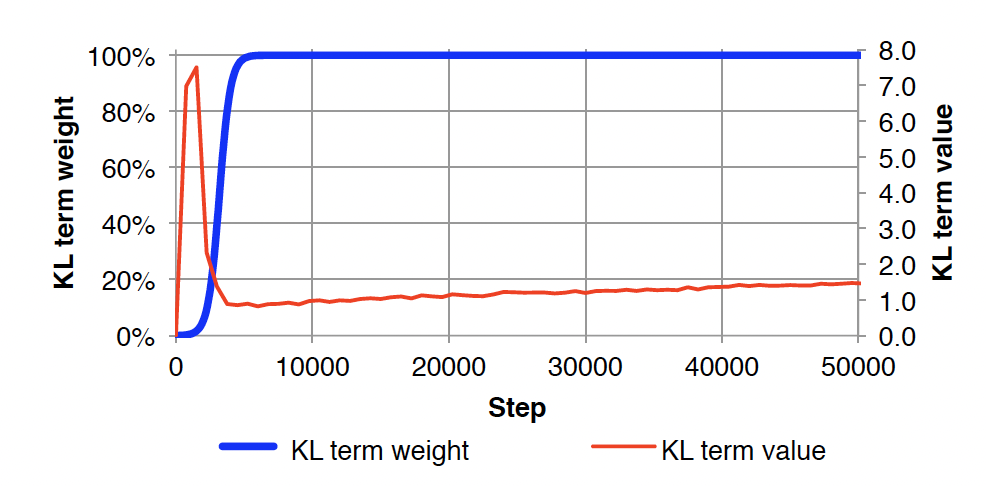
図 2 は,KL コスト焼きなましを導入した Penn Treebank (Marcus et al.,1993) 言語モデリングにおいて,最初の 50k ステップの学習における KL コスト項の振る舞いを示したものである。 この例では,我々がよく観察するパターンを再現している。 KL は学習初期に急上昇し,その後 KL ダイバージェンスのペナルティを受け始めると大幅に低下し,最終的には再び上昇し,$z$ に情報を凝縮することを学習すると収束する 。
3.3.2 単語ドロップアウトと履歴なし復号化
符号化のペナルティ項を弱めるだけでなく,復号化の弱体化も実験している。 RNNLMsや 系列自己符号化器と同様に,学習中の復号化器は実際の前単語を条件として各単語を予測する。 復号化を弱めるには,学習中にこの条件付け情報の一部または全部を削除するのが自然な方法である。 これは条件付けされた単語トークンの一部を一般的な未知の単語トークン unk とランダムに置き換えることによって行う。 これにより,モデルは潜在変数 $z$ に依存して良い予測をするようになる。 この手法は,単語ドロップアウト (Iyyer et al.,2015; Kumar et al.,2015) の変形であり,特徴抽出器ではなく,復号化器に適用したものである。 また,復号化器の入力単語埋め込みに適用される標準ドロップアウト (Srivastava et al.,2014) も実験したが,これはモデルが潜在変数を使用することを学習するのに役立たなかった。
この手法は 保持率 $k\in[0,1]$ によってパラメータ化されている。 我々は,このパラメータを,我々の VAE とベースライン RNNLM の両方について調整する。 $k=0$ の場合,復号化器は何も入力しないため,これまでに生成された単語数のみを条件とすることができ,$z$ を使用せずにモデル化できる分布の種類が極端に制限されるモデルが出来上がる。
4. 結果 言語モデリング
本節では,大域的潜在変数がこの標準的な課題に有用であるかどうかを見るために Penn Treebank の言語モデリング実験について報告する。 このため,我々は変分下界の KL ダイバージェンス項によって測定されるように,潜在変数に非自明な量を包含するモデルにハイパーパラメータ探索を制限している。
4.1 結果
コーパスは標準的な 訓練と検証分割を用い,表 2 にテストセットの結果を報告する。 この結果は,各モデルが開発セットで最も良い性能を示した学習ステップでの学習と検証セットの性能を反映している。 また,VAE は検証データ尤度の変分下界を,RNNLM は検証データ尤度を正確に評価することができるため,真のテスト尤度を報告している。 この相違により VAE は不利になる可能性がある。
標準的な設定では VAE は RNNLM のベースラインよりもわずかに性能が劣るが,潜在空間を限定的に利用することに成功している。 再構成コスト (99) は RNNLM のベースラインより優れているが,KL ダイバージェンスコストが 2 であり,これを補うことができる。 ワードドロップアウトとコストアニーリングの両方を行わない標準的な設定で VAE を訓練すると,ベースライン RNNLM と同等の性能を持ち,KL ダイバージェンスがゼロのモデルを確実に得ることができます。
潜在変数が,より抽象的な大域的特徴に加えて,文の内容を完全に符号化できることを示すために,前のトークンを条件としない無入力復号化器の数値も示している (単語のドロップアウト維持率 0 に対応) 。 この領域では,変分下界はかなり大きな KL 項を含み,弱体化した RNNLM よりも実質的な改善を示していることがわかるが,この設定では基本的に一文統計の利用に限定される。 入力なし復号化器は,標準的な復号化器より弱いものの,文生成過程が完全微分可能という興味深い性質を持っている。 この種の生成モデルの進歩は,微分可能な生成器を必要とする敵対的学習法を用いながらテキストを生成する手段として有望であると考えられる。
前節で述べた無入力復号器を含む手法でも,コスト関数の KL ダイバージェンス項が再構成項を支配するようなモデルを学習することはできなかった。 このことは RNNLM のように単純な局所統計量を用いてデータ分布を因数分解する方がまだ実質的に学習しやすく,復号化器はその情報がこれらの局所統計量で効果的に記述できない場合にのみ $z$ の情報を符号化するように学習することを示唆している。
5. 結果 欠落語の推定
我々は VAE が持つ大域的な文の特徴により,既知の文に含まれない単語を推定する課題に特に適していると主張する。 本節では,単語置換の手法と,敵対的訓練に着想を得た新しい評価戦略を紹介する。 定性的には VAE は同じ計算量でより多様で妥当な代入を行うことができるが (表 3 の例参照),正確な定量評価には難解な尤度計算が必要であることが分かる。 そこで,我々は新しい評価方法を導入し,この問題を回避した。
標準的な RNNLM は強力な生成モデルであるが,尤度計算と復号が連続的であるため,既知の単語から未知の単語を推定する (代入課題) には不向きである。 未知語のすべてが復号系列の最後に現れるような特殊な場合を除き,欠落した変数に対する事後サンプリングは,最小の語彙を除き,困難である。 サイズ $V$ の語彙の場合,Gibbs サンプリングまたは条件モードの反復の 1 ステップあたり $O(V)$ 回の完全なRNN 推論を必要とする。 さらに RNNLM によって与えられるグラフィカルモデルの方向性のため,未知の変数と既知の下流変数の間の情報を伝播するために,多くのステップのサンプリングが必要となる可能性がある。 VAE は,サンプリングや写像代入計算において,同じように難解な問題を抱えるが,大域的な潜在変数と扱いやすい認識モデルを持っているため,すべての変数間の情報をより容易に伝播させることができる。
この実験とその後の分析では Kiros et al.(2015) で紹介された Books Corpus でモデルを学習する。 これは 12k の電子書籍のテキストを集めたものであり,ほとんどがフィクションである。 プルーニング後のデータセットには約 80 M 文が含まれる。 我々は,このはるかに大きなデータ量が,より小さな標準的な言語モデリングデータセットよりも主観的に興味深い生成モデルを生成することを見出した。 このモデルの学習には,特に指定がない限り 75% の固定単語ドロップアウト率を用いている。 このモデル (VAE と RNNLM) は言語モデルとして学習され,VAE では学習時に依存関係を短くするために右から左へ復号化される。 512 の隠れユニットを使用した。
5.1 推論方法
2 つのモデルから代入課題を生成するために RNNLM ではビームサイズ 15 のビームサーチを,VAE ではビームサイズ 5 の 3 ステップの探索を行う近似反復条件モード (Besag, 1986) を使用する。
これにより,両モデルで同じ計算量を比較することができる。
その結果 VAE に対する復号をいくつかの連続したステップに分けることが,変数間の情報を伝播させるために必要であることがわかった。
条件付き反復モードは,条件付き分布を交互に最大化することにより,変数集合の最大結合割り当てを求める手法であり k-means (Kearns et al.,1998) のような ハードEM アルゴリズムの一般化である。
近似的な反復条件モードでは,まず未知語は unk トークンに初期化する。
次に,認識モデルから潜在変数をそのモードに割り当て,未知語を割り当てるために制約付きビームサーチを交互に実行する。
両生成モデルは右から左へ文を解読するように学習され VAE の学習に関わる依存関係を短くし,各文の最後の20% をインプットする。
これにより RNNLM が帰納バイアスに最も苦しむ領域で,大域的潜在変数の利点を示すことができる。
5.2 敵対的評価
ノンパラメトリック二標本検定と同様に生成モデルのための敵対的学習方法からヒントを得て (Goodfellow et al.,2014; Li et al.,2015b; Denton et al.,2015; Gretton et al.,2012),真の文末との区別性を調べることによってインプット文末を評価した。 離散 RNN 復号化器の微分不可能性から,訓練時に敵対的基準を容易に適用できない。だが,生成文と真文を分離する判別関数を訓練することにより,非常に柔軟なテスト時評価を定義し,敵対的エラーを定義することが可能である。
2 つの分類器を訓練した: Bag-of-Unigrams ロジスティック回帰 と LSTM ロジスティック回帰,である。両者は入力文を読み,最後の eos トークンを見た後に二値予測を生成する。 これらの分類器は 80/10/10 の 320k 文 の train/dev/test 分割で早期停止を用いて学習し,コーパスから 50% の完全な文 (正事例) と 50% の偽の完全な文 (負事例) からなるデータセットを構築する。 敵対的誤差は,識別器の理想的な精度 (50% すなわち識別不可能なサンプル) と実際に達成された精度との間のギャップとして定義される。
5.3 結果
この実験の結果 RNNLM は文の最後のトークンを生成する際,RNN の初期無条件分布 $P(x_{1}|\text{Null})$ によって与えられる上位 15 個のトークン以外のものを選択することができない。 なぜなら,条件となるものをまだ生成せず,ビームサイズが 15 であるためである。 表 4 は,この弱点により RNNLM は VAE よりもはるかに多様性に欠けるサンプルを生成し,それに応じて敵対的分類器に対して苦戦していることを示している。 さらに,独立に訓練された言語モデルを用いて,文全体に与えられた得点と推定された補完を含んでいる。 尤度の結果は同等だが RNNLM は「彼は言った he said」のような一般的な高確率の語尾を好むため,負の対数尤度が若干低くなっている。 RNNLM によって生成された文の尤度を測定することは,モデルのパワーを測定する良い方法ではないが,RNNLM は,典型的な局所統計量を優先して,高品質の代入語を生成できることを実証している。 したがって,敵対的評価の下では,我々のモデルは潜在変数を通して効率的に情報を双方向に伝搬させることができるため,ベースラインを大幅に上回る性能を発揮する。
6. 変分モデルの分析
ここでモデルのより定性的な分析に移る。 我々の復号化モデル $p(x|z)$ は洗練された RNNLM なので,単に有向グラフモデルからサンプリングしても (最初に $p(z)$,次に $p(x|z)$) データが潜在空間と復号化器のそれぞれによってどのくらい説明されているかについてはあまりわからないだろう。 その代わりに,評価のここでは,ガウス事前分布からサンプリングするが $p(x|z)$ すなわち $z$ に条件付けられた RNNLM のための貪欲な決定論的復号化器を使用する。 これにより,データ分布の分散のどの程度が,復号化器ではなく,分布ベクトル $z$ によって捕捉されているかを知ることができる。 興味深いことに,これらの結果は,生成された言語の大きな変動がこの手順に従うことによって達成されることを定性的に示している。 付録では,小さなテキストの分類課題に関するいくつかの結果を示す。
6.1 単語脱落の影響分析
この実験では,書籍コーパスで学習し,そのコーパスから取り出した 1 万文のテストセットでテストを行った。 その結果,学習セットとテストセットの性能は非常によく似ていることがわかった。 図 3 では,単語の削除が変分下界に与える影響を KL ダイバージェンスと交差エントロピーの成分に分解して検証している。 訓練時に指定された保持率の単語を削除し,テスト時には 0% 設定を除いて全ての単語を入力として供給する。
各実行でハイパーパラメータの再チューニングを行わないため,ドロップアウトのないモデルは $z$ の情報が非常に少ない (すなわち KL 成分が小さい) 結果となった。 単語のドロップアウトの保持率を下げると,潜在変数に格納される情報量が増え,モデル全体の尤度が多少劣化することがわかる。 4 節の結果から,潜在的変数を持たないモデルは,重い単語脱落がある場合,著しく性能が低下することがわかる。
また KL の増加により,純粋に連続サンプリングから意味のある文が生成できることを示すため,サンプルを定性的に評価した。 我々の復号化モデル $p(x|z)$ は洗練されたRNNLM なので,有向グラフモデルから単純にサンプリングしても (最初に $p(z)$ 次に $p(x|z)$),学習ベクトルと言語モデルでどの程度データが説明されているかはわからないだろう。 その代わりに,定性的評価のこの部分では,ガウス事前分布からサンプリングしますが,各トークン $x_{t}=\operatorname{argmax}{x{t}}p(x_{t}|x_{0,\ldots,t-1}, z)$ を取り,$x$ の貪欲な決定論的復号化器を使用する。 これにより,データ分布の分散のうち,局所的な言語モデルの依存性ではなく,分布ベクトル $z$ によってどの程度捕捉されているかを把握することができる。
表 5 に示すこれらの結果は,この手順に従うことで,生成される言語の大きなバリエーションが得られることを定性的に示している。 低レベルでは $z$ によって説明される分散はごくわずかであり,ガウス型サンプルに適用される貪欲な復号化では多様な文が生成されないことがわかる。 単語のドロップアウト量を増やし,$z$ がより多くの情報を符号化するようにすると,文はより多様になる。 だが,ある点を超えると,単語の繰り返しや他の非文法的な徴候が現れ始める。 このように,完全に脱落した復号化器の場合でも,このモデルは 1 gram の分布には存在しない高次の統計量を捕らえることができる。
さらに 表 6 では 75% の単語保持率を持つモデルにおいて,潜在的なガウス空間からより低い確率のサンプルを使用することの効果を検証している。 ガウス分布に体積保存変換を行い,いくつかの固有空間を最大 4 倍まで拡張することで,より低い確率のサンプルを見つけることができる。 この変換は,事前分布の下ではあまりありえないが,分布の末尾に到達するサンプルを作成する効果がある。 我々は,行列の要素が [-c,c] の一様分布から抽出されたランダムな線形変換を使用し,c は望ましい特性 (我々の実験では 0.1) を与えるように選択される。 ここで,文ははるかに典型的ではないが,大部分は文法的であり,明確なトピックを維持していることがわかる。 これは,潜在変数がまれな文であっても豊富な種類の大域的な特徴を捉えていることを表している。
6.2 事後関係からのサンプリング
無条件サンプルの生成に加えて,様々な文 $x$ に対して事後ベクトル $p(z|x)$ から復号した文を調べることができる。 モデルは決定論的なコードではなく,分布を生成するように正則化されているので,入力を正確に記憶して往復 (ラウンドトリップ) することはない。 その代わり,表 7 の事後サンプルを調べることで,モデルが何を類似文とみなしているかを見ることができる。 このコードは,トークンの数と各トークンの品詞に関する情報,およびトピック情報を捉えているようである。 文が長くなるにつれて,往復した文の忠実度は減少する。
6.3 線形補間 Homotopies
変分自己符号化器を用いることで,符号化空間からの連続的なサンプルに対して貪欲な復号を用いて文を生成することができる。 さらに,符号空間の体積充填性と滑らかさにより,文間のホモトピー (線形補間) の概念を初めて検証することができる。 ここで 2 つの符号 $z_{1}, z_{2}$ 間のホモトピーとは,それらの間の直線上の点の集合で $t\in[0,1]$ に対して $z(t)=z_{1}(1-t)+z_{2}t$ を包括したものである。 同様に,コード $z_{1}$ と $z_{2}$ から (貪欲に) 復号された二つの文の間のホモトピーは,線上のコードから復号された文の集合となる。 これらのホモトピーを調べることで,コード空間の近傍がどのようなものか,自己符号化器がどのように情報を整理し,何を 2 文間の連続変形とみなしているか,を知ることができる。
標準的な非変分 RNNLM はこのようなホモトピーを行う方法がない。
だが,バニラ系列自己符号化器はこれを行うことができる。
しかし,前述したように 表 1 の系列自己符号化器で作られたホモトピーを調べると,文の切り替えが鋭く,非文法的な中間文になっていることが分かる。
これは VAE が滑らかで空間を 埋める 表現を学習するという我々の直感の根拠となる。
表 8 (および付録の追加表) では,コードのほとんどがトークンの語数や品詞などの構文情報を含んでおり,中間文はすべて文法的であることがわかる。
また,いくつかのトピック情報は経路上の近隣で一貫している。
さらに,構文やトピックは似ているが,例えば「痛みは耐えられない」対「その考えは私を微笑ませた」のように感情の価数が反転している文は,類似の埋め込みを持つことがある。
これは単一単語の埋め込みで観察されている現象である (例えば 悪い と 良い のベクトルは,その分布特性が似ているのでしばしば非常によく似ている)。
7. まとめ
本論文では,自然言語文に対する変分自己符号化器の利用について紹介した。 本論文では,変分自己符号化器を用いた自然言語文の学習と,欠落単語を効率的に埋め込むための新しい手法を提案した。 また,本モデルが学習する潜在空間を解析し,純粋な連続サンプリングにより一貫性のある多様な文を生成できること,文間を滑らかに補間する解釈可能なホモトピーを提供できることを明らかにした。
将来的には,潜在的な変数をスタイルと内容の別々の成分に分解すること,外部的な特徴を条件として文を生成すること,テキスト内包のような言語理解課題のために半教師付き方式で文埋め込みを学習すること,敵対的評価を超えて完全な敵対的学習目標に到達することを期待している。
付録
A.1. テキスト分類
VAE によって発見された表現の構造をさらに調べるために,言い換え検出と質問タイプ分類の分類実験を行った。 書籍コーパスに対して,隠れ状態サイズ 1200 の VAE を学習し,抽出された文ベクトルとしてモデルの事後平均を使用した。 これらの平均に対して Kiros et al.(2015) と同じ実験プロトコルで分類器を学習させた。
A.1.1. 言い換え検出
言い換え検出課題には Microsoft Research Paraphrase Corpus (Dolan et al.,2004) を使用した。 Kiros et al.(2015) と同様に文対の文ベクトルから 2 つのベクトルの要素毎の積と要素毎の差の絶対値を連結して特徴を計算する。 l2 正則化ロジスティック回帰分類器を学習し,交差検証法を用いて正則化の強さをチューニングした。
この課題の結果を表 9 に示し,いくつかの先行モデルと比較する。 Feats は Socher et al.(2011) の語彙化ベースラインである。 RAE はその研究の再帰的自己符号化器を使用し,DP は対毎特徴を計算するために彼らの動的プーリングステップを追加したものである。 ST は単方向 skip-thought モデル,BI-ST は双方向 skip-thoughtモデル, combine-ST はそれらの特徴を連結したものを用いている。 また,語彙素性と 2 種類の分散素性を連結する実験も行った。
その結果,本特徴は単独では skip-thought 特徴量より若干悪く,再帰的オートエンコーダ特徴量より若干良い性能を示し,skip-thought 特徴量と単純に連結した場合には補完的で強い性能を発揮することが分かった。
A.1.2. 質問分類
Li and Roth (2002) の TREC Question Classification データセットに対する実験も行う。 Kiros et al.(2015) に従い,正則化を設定するために 10-fold cross-validation で l2-正則化ソフトマックス分類器を学習する。 このような線形分類器を使用すると,VAE の隠れコード上のガウス分布が線形分離性を阻害する可能性が高いため,ここでの我々の表現に不利になる可能性があることに注意。
表 10 に結果を示した。 ここで AE はプレーン系列自己符号化器である。 Bag of word vectors (cbow, Zhao et al.,2015) や skip-thought (st) の結果と比較した。 また RNN 分類器 (Zhao et al., 2015) や CNN 分類器 (Kim, 2014) とも比較したが,これらは我々のモデルとは異なり,エンドツーエンドで最適化されたものであった。 この場合 VAE コードの性能を cbow より良くすることはできなかったが,系列自己符号化器からの特徴量を上回った。 これは,次文予測というスキップソートの学習目的がこの課題によく合致しているためと思われる。 スキップソートは本質的に,本の物語から得た暗黙のオープンな質問に対応する文を生成するようモデルを訓練した。 2 つの表現を組み合わせても,基本的な skip-thought モデルに対する性能向上は見られなかった。
A.2 ハイパーパラメータのチューニング
各モデルのハイパーパラメータを,開発セットのデータに対して自動ベイズハイパーパラメータチューニングアルゴリズム (Snoek et al.2012 に基づく) を用いて広範囲にチューニングした。 各ハイパーパラメータのセットで 10 時間モデルを実行し,12 個の実験を並行して行い,200 回実行した後に最適なハイパーパラメータのセットを選択した。 言語モデリング実験の結果は,次ページの 表 11 に示したとおりである。
A.3 追加のホモトピー
次ページの 表12 は,我々のモデルから得られた追加のホモトピーである。 中間文はほぼ常に文法的であり,終点文の間を補間するように局所近傍に一貫したトピック,語彙,構文情報を含むことが多いことが分かる。 このモデルは恋愛小説などのフィクションを対象としているため,話題はかなり劇的なことが多い。