ベイズ推論問題 MCMC と変分推論

統計学におけるベイズ推定問題の概要

Joseph Rocca, Jul 1, 2019

1. はじめに

ベイズ推定は，統計学における主要な問題であり，多くの機械学習法においても遭遇する問題である。 例えば，分類のためのガウス混合モデルやトピックモデリングのための Latent Dirichlet Allocation などは，いずれもデータをフィッティングする際にこの問題を解決する必要があるグラフィカルモデルである。

一方で，ベイズ推定問題は，モデルの設定 (仮定，次元数など) によっては，非常に難しい問題になることがある。 大規模な問題では，厳密な解を得るためには膨大な計算が必要となり，しばしば手に負えなくなる。この問題を克服し，高速でスケーラブルなシステムを構築するためには，いくつかの近似技術を使用する必要がある。

この記事では，ベイズ推論の問題に取り組むために使用できる 2 つの主な手法について説明する: サンプリングベースのアプローチである Markov Chain Monte Carlo (MCMC) と，近似ベースのアプローチである変分推論 Variational Inference (VI) である。

1.1 概要

最初の節では，ベイズ推論問題について説明し，この問題が自然に現れる古典的な機械学習の応用例をいくつか見てみる。 そして第 2 章では，この問題を解決するためのグローバルな MCMC 手法を紹介し，2 つの MCMC アルゴリズムについて詳細を述べる。 Metropolis-Hasting と Gibbs Sampling である。 最後に第 3 章では，変分推論を紹介し，パラメータ化された分布群に対する最適化過程を経て，どのように近似解が得られるかを見ていく。

注: (∞) でマークされた節はかなり数学的なので，このポストの全体的な理解を妨げることなくスキップすることができる。 また，この記事では，$p(.)$ は，文脈に応じて，確率，確率密度，確率分布のいずれかを表すために使用されていることに注意。

2. ベイズ推論問題

本節では，ベイズ推論問題を提示し，いくつかの計算上の困難さを議論した後，この問題に遭遇するトピックモデリングの具体的な機械学習手法である Latent Dirichlet Allocation の例を示す。

2.1 推論とは何か？

統計的推論とは，観察したものに基づいて，観察していないものについて学ぶことである。 言い換えれば，母集団または母集団の標本で観察された変数 (多くの場合，影響) に基づいて，母集団のいくつかの潜在的な変数 (多くの場合，原因) について， 時間的推定，信頼区間または分布推定などの結論を導く過程である。

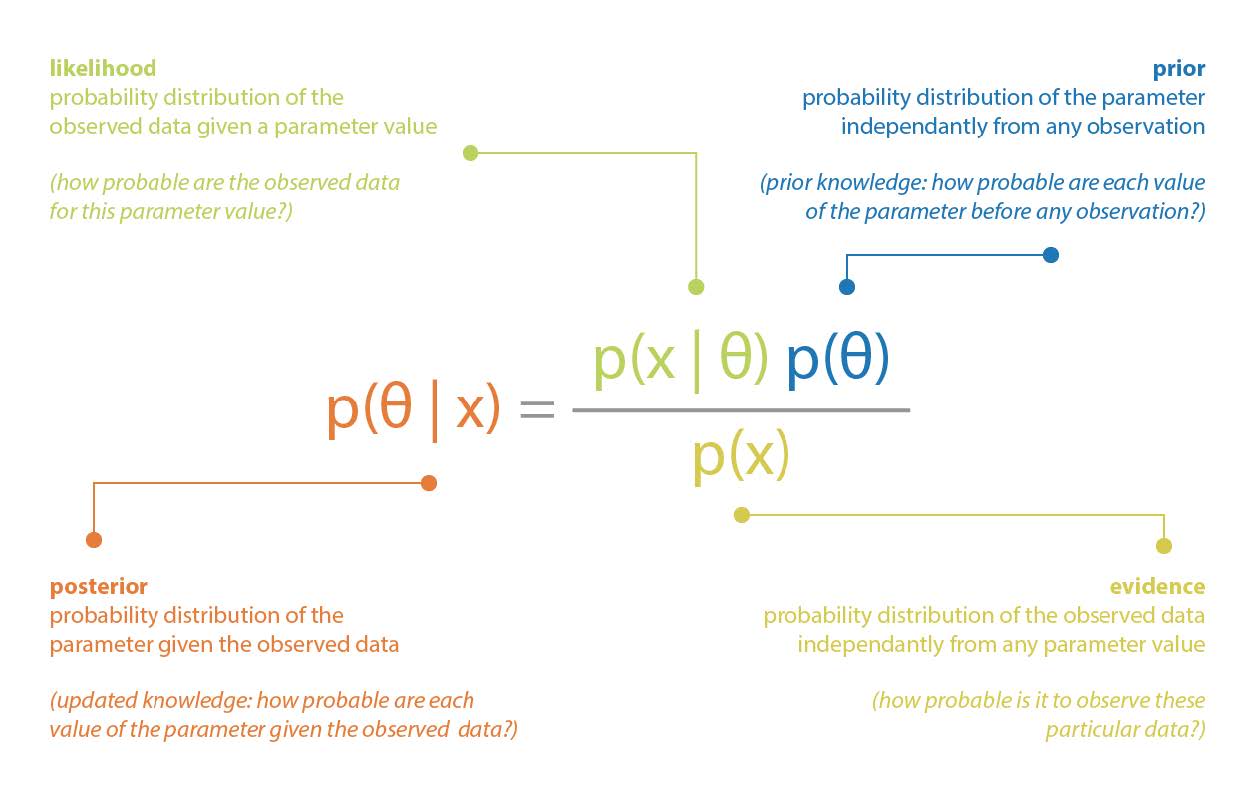
特にベイズ推論は，ベイジアンの視点で統計的推論を行う過程である。 つまり，ベイズのパラダイムは，確率分布でモデル化された事前知識が，別の確率分布でモデル化された不確実性を持つ新しい観測結果が記録されるたびに更新される，統計的／確率的なパラダイムである。 ベイジアンパラダイムを支配する全体的な考え方は，更新された知識 (事後)， 事前知識 (事前)，および観測から得られる知識 (尤度) の間の関係を表現する，いわゆるベイズ定理に組み込まれている。

古典的な例としてパラメータのベイズ推論がある。 データ $x$ が未知のパラメータ $\theta$ に依存する確率分布から生成されるモデルを想定してみよう。 また，パラメータ $\theta$ について，確率分布 $p(\theta)$ として表現できる事前知識を持っているとする。 そして，データ $x$ が観測されたとき，ベイズの定理を用いてこのパラメータに関する事前知識を次のように更新することができる:


図 1. 観測されたデータからパラメータを推定する際に適用されるベイズの定理の説明

2.2 計算上の問題点

ベイズの定理によれば，事後評価の計算には，事前，尤度，証拠の 3 つの項が必要であるとされている。 最初の 2 つは，想定されるモデルの一部であるため，簡単に表現することができる (多くの状況では，事前と尤度は明示的に知られている)。 しかし，3 つ目の項，つまり正規化係数は，以下のように計算する必要がある:

\[p(x)= \int_{\theta}p(x\vert\theta)\;p(\theta)\;d\theta.\]

この積分は低次元ではそれほど困難なく計算できるが，高次元では難解になることがある。 この場合，事後分布を厳密に計算することは現実的に不可能であり，この事後分布を知る必要がある問題 (例えば，平均の計算など) の解を得るためには，何らかの近似的な手法を用いなければならない。

ベイズ推定問題には，例えば変数が離散的である場合の組合せ問題など，他の計算上の困難が生じることがあることに気付くことができる。 これらの困難を克服するために最もよく使われるアプローチとして，マルコフ連鎖モンテカルロ法と変分推論法がある。 この記事の後半で，特に「正規化因子問題」に焦点を当てて，この 2 つのアプローチについて説明するが，ベイズ推定に関連する他の計算上の困難に直面したときにも，これらの方法が重要になることを覚えておく必要がある。

次節以降でもう少し一般化するが，$x$ が所与であり，パラメータとして扱えるので，$\theta$ の確率分布が正規化因子まで定義されている状況に直面することができる。

\[\pi_{x}(\theta) \equiv p(\theta\vert x)\propto p(x\vert\theta)\;p(\theta)\equiv g_{x}(\theta)\]

次の 2 節で MCMC と VI を説明する前に，潜在ディレクリ配置 Latent Dirichlet Allocation を用いた機械学習におけるベイズ推論問題の具体例を挙げる。

2.2.1 例

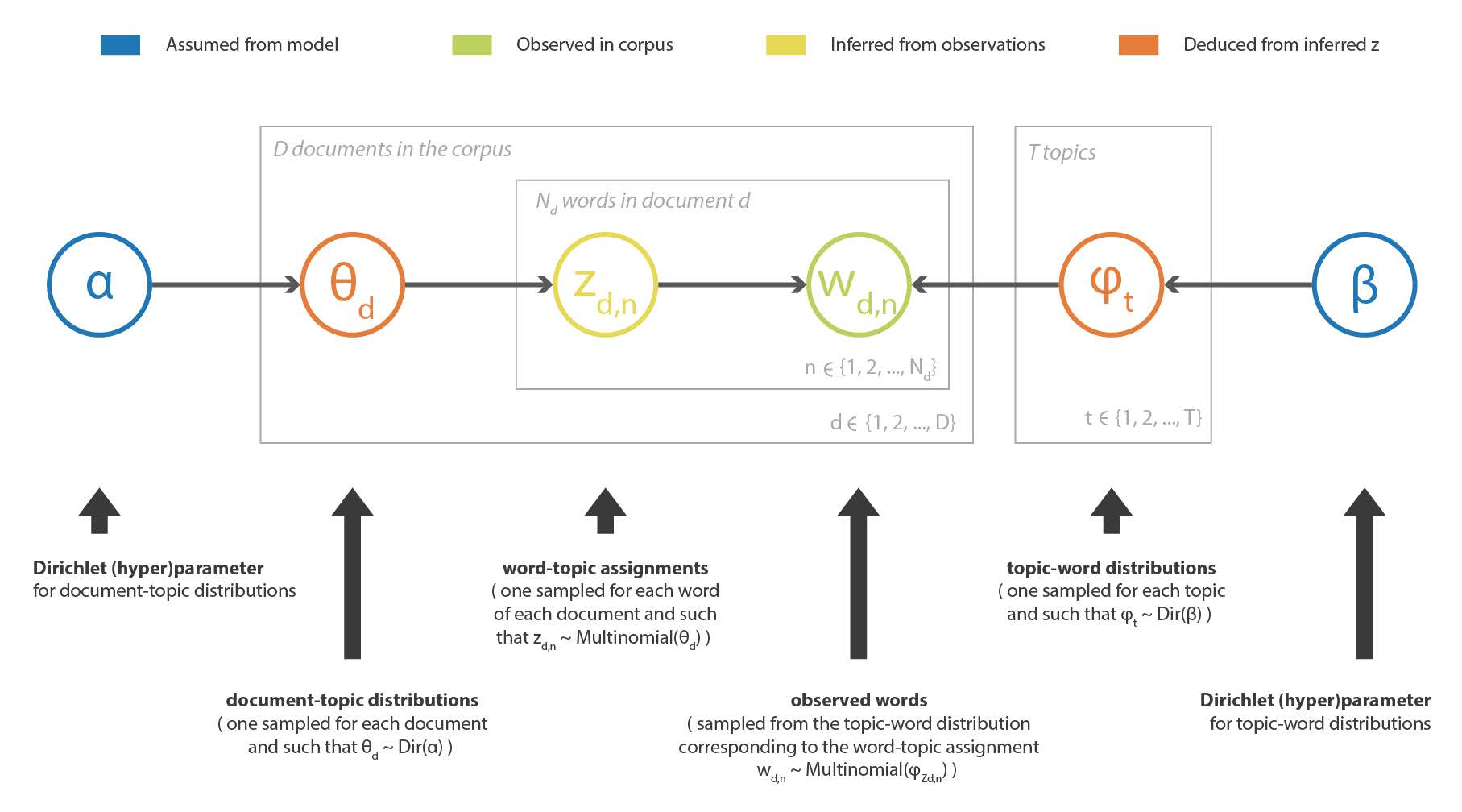
ベイズ推定問題は、例えば確率的グラフィカルモデルを仮定した機械学習手法において，ある観測値が与えられたときに，そのモデルの潜在変数を復元したい場合に，自然に現れるものである。 トピックモデリングでは，LDA (Latent Dirichlet Allocation) 法がコーパス中のテキストの記述のためにこのようなモデルを定義している。 したがって，サイズ V の完全なコーパスの語彙と与えられたトピック数 T が与えられたとき，このモデルは以下のように仮定する:

  • 各トピックについて，語彙に対する「トピック-単語」確率分布が存在する(Dirichlet 事前分布を仮定)。
  • 各文書に対して，トピックに対する「文書-トピック」確率分布が存在する (これもディリクレ事前分布を仮定)。
  • 文書内の各単語は，まず文書の「文書-トピック」分布からトピックを抽出し，次に，抽出されたトピックに付随する「トピック-単語」分布から単語を抽出するようにサンプリングされる。 <!– - there exists, for each topic, a “topic-word” probability distribution over the vocabulary (with a Dirichlet prior assumed)
  • there exists, for each document, a “document-topic” probability distribution over the topics (with another Dirichlet prior assumed)
  • each word in a document have been sampled such that, first, we have sampled a topic from the “document-topic” distribution of the document and, second, we have sampled a word from the “topic-word” distribution attached to the sampled topic –>

この手法の目的は，観測されたコーパスの潜在的なトピックと，各文書のトピック分解を推定することである (モデルで仮定されたディリクレ事前分布に由来)。 LDA の詳細は省略するが，非常に大雑把に言えば，コーパスに含まれる単語のベクトルを $w$, これらの単語に関連するトピックのベクトルを $z$ とすると，観測された $w$ に基づいてベイズ的手法で $z$ を推定することである。

\[p(z\vert w) =\frac{p(w\vert z)p(z)}{p(w)} = \frac{p(w\vert z)p(z)}{\int_{z}p(w\vert z)\;p(z)\;dz}.\]

ここでは，次元が大きいために正規化因子が絶対的に困難であることに加え，(問題のいくつかの変数が離散的であるため) 組合せ的な問題に直面し，MCMC か VI を使って近似解を得る必要がある。 トピックモデリングとその基礎となるベイズ推定問題に興味のある読者は LDA に関する この参考文献 を参照。


図 2. Latent Dirichlet Allocation の説明図

3. マルコフ・チェーン・モンテカルロ法 (MCMC)

先に述べたように，ベイズ推定問題を扱う際に直面する主な困難の 1 つは，正規化因子に由来するものである。 本節では，この問題とベイズ推定に関連する他のいくつかの計算上の困難を克服するための可能な解決策を構成する MCMC サンプリング法について説明する。

3.1 サンプリングの方法

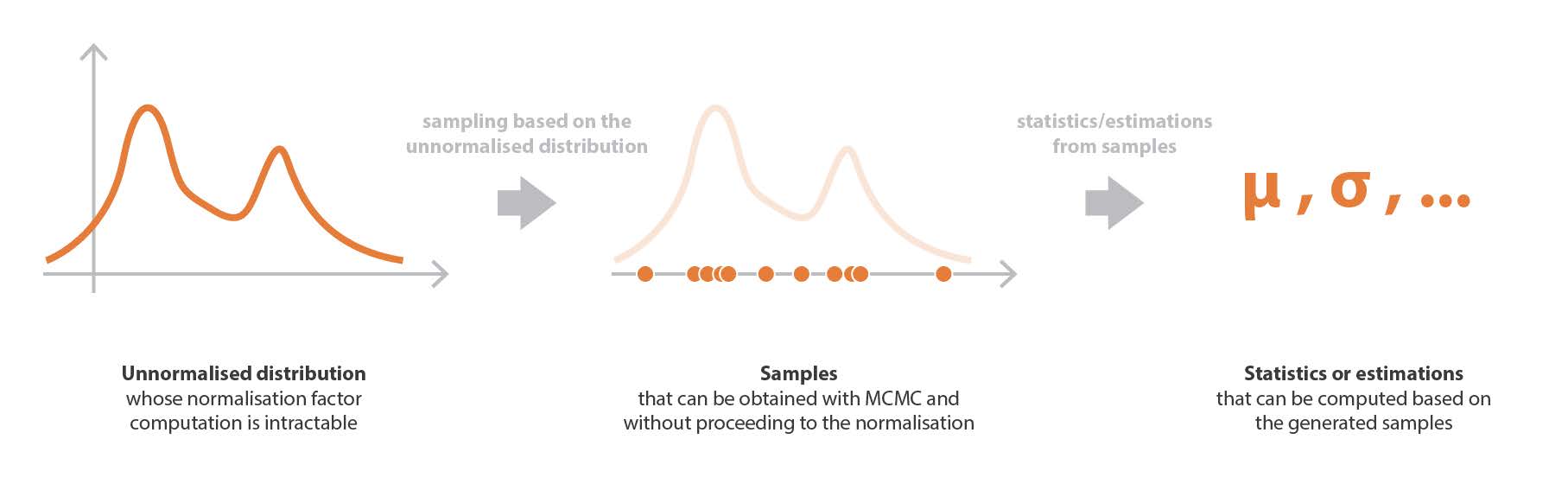
サンプリング法の考え方は以下の通りである。 まず，ある係数まで定義された確率分布からサンプルを抽出する方法 (MCMC) があるとする。 すると，事後確率を含む難解な計算を扱う代わりに，この分布からサンプルを得て (正規化されていない部分の定義だけを用いて)， これらのサンプルを用いて平均や分散などの様々な時間的統計量を計算したり，カーネル密度推定によって分布を近似したりすることができる。

次節で述べる VI 法とは対照的に，MCMC 法は調査した確率分布 (ベイズ推論の場合の事後値) に対してモデルを仮定しない。 その結果，これらの方法はバイアスは低いが分散が大きく，ほとんどの場合，VI から得られる結果よりもコストがかかるが，より正確であることを意味する。

本節の最後に，今述べたサンプリング過程は，ベイズ推定の事後分布に限定されるものではなく，より一般的に，確率分布がその正規化因子まで定義されているあらゆる状況で使用できることを，もう一度概説する。

図 3. サンプリング手法（MCMC）の説明図。

3.2 MCMC の考え方

統計学において，マルコフ連鎖モンテカルロ法は，与えられた確率分布からサンプルを生成することを目的としている。 この手法の名前の「モンテカルロ」の部分はサンプリングの目的からきており「マルコフ連鎖」の部分はこれらのサンプルを得る方法からきている (読者は マルコフ連鎖についての入門記事 を参照)。

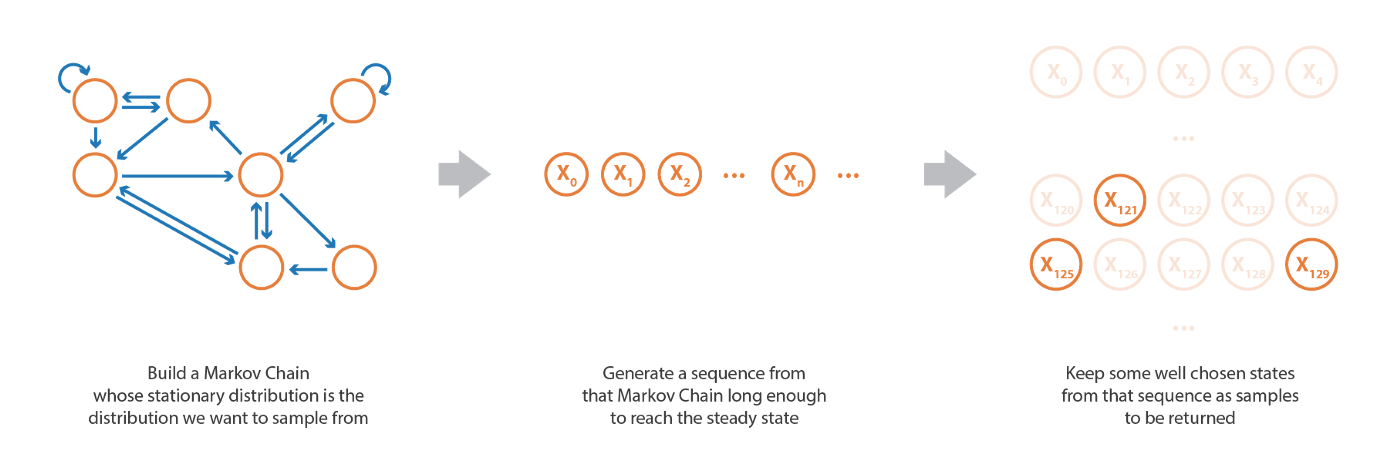
サンプルを生成するためには，サンプリングしたい定常分布を持つマルコフ連鎖を設定することである。 そして，そのマルコフ連鎖から，定常状態に (ほぼ) 到達するのに十分な長さのランダムな状態列をシミュレートし，生成されたいくつかの状態をサンプルとして保持することができる。

確率変数の生成手法の中でも MCMC はかなり高度な手法であり (他の手法については GAN に関する投稿 ですでに説明した)，乗法定数までしか定義できない非常に難しい確率分布からサンプルを取得することが可能 である。 MCMC で正規化されていない分布からサンプルを得ることができるという直感に反する事実は，これらの正規化因子に影響されないマルコフ連鎖を定義する特定の方法からきています。


図 4. マルコフ連鎖モンテカルロ法は，因子まで定義できる難しい確率分布からサンプルを生成することを目的としている

3.3 マルコフ連鎖の定義

MCMC のアプローチ全体は，サンプリングしたいものを定常分布とするマルコフ連鎖を構築する能力に基づいている。 これを実現するために，メトロポリス・ヘイスティングとギブスサンプリングのアルゴリズムは，両方ともマルコフ連鎖の特別な性質である可逆性を利用する。

遷移確率を持つ状態空間 E 上のマルコフ連鎖を以下のように定義する:

\[\kappa(\alpha,\beta)\equiv p(X_ {n+1}=\beta\vert X_ {n}=\alpha),\]

次のような確率分布 $\gamma$ が可逆であると言う。

\[\kappa(\alpha,\beta)\gamma(\alpha)=\kappa(\beta,\alpha)\gamma(\beta)\hspace{2cm}\forall \alpha,\beta\in E\]

このようなマルコフ連鎖では，以下を容易に確認できる

\[\int_ {\beta\in E}\kappa(\beta,\alpha)\gamma(\beta)\,d\beta=\int_ {\beta\in E}\kappa(\alpha,\beta)\gamma(\alpha)\,d\beta=\gamma(\alpha)\]

であり $\gamma$ は定常分布 (マルコフ連鎖が既約なら唯一) である。

ここで，標本化したい確率分布 $\pi$ が，ある因子までしか定義されていないと仮定する

\[\pi(\cdot)=C\times g(\cdot)\propto g(\cdot)\]

(ここで C は未知の乗法定数)。 以下の同値が成立することに気づくことができる。

\[\begin{aligned} \kappa(\alpha,\beta)\pi(\alpha) &= \kappa(\beta,\alpha)\pi(\beta) \hspace{1cm}\forall \alpha,\beta\in E\\ \Leftrightarrow \kappa(\alpha,\beta)g(\alpha) &=\kappa(\beta,\alpha)g(\beta)\hspace{1cm}\forall\alpha,\beta\in E\\ \end{aligned}\]

そして，最後の等式を検証するために定義された遷移確率 $\kappa(\cdot,\cdot)$ を持つマルコフ連鎖は，予想通り $\pi$ を定常分布として持つことになる。 このように，明示的に計算できない確率分布 $\pi$ を定常分布に持つマルコフ連鎖を定義することができる。

3.4 ギブスサンプリング遷移 (∞)

定義したいマルコフ連鎖が D 次元で，次のようなものであるとする:

\[X_ {n} = \left(X_ {n,1}, X_ {n,2},\ldots, X_ {n,D}\right)\]

ギブスサンプリング法 は，結合確率が難解でも，ある一次元の条件付き分布が他の次元から与えられると計算できる，という仮定に基づいている。 この考え方に基づき，反復回数 $n+1$ において，次に訪れる状態が以下のような処理で与えられるように遷移が定義される。

まず $X_ {n}$ の D 次元の中からランダムに整数 $d$ を選択する。 次に，他の次元を固定とした場合の条件付き確率に従って，その次元の新しい値をサンプリングする。

\[d\sim \text{Uniform}(\{1,2,\ldots,D\}), X_ {(n+1),j}= X_ {n,j}\hspace{1cm}\forall j\ne d\text{ and }X_ {(n+1),d} \sim \pi_ {d}(\cdot\vert X_ {n,\neg d})\]

ここで

\[\pi_ {d}(\cdot\vert X_ {n,\neg d}) =\frac{\pi(X_ {n,1},\ldots,X_ {n,(d-1)}\cdot X_ {n,(d+1)},\ldots, X_ {n,D})}{ \int \pi(X_ {n,1},\ldots,X_ {n,(d-1)}\cdot X_ {n,(d+1)},\ldots, X_ {n,D})\,du} =\frac{g(X_ {n,1},\ldots,X_ {n,(d-1)}\cdot X_ {n,(d+1)},\ldots, X_ {n,D})}{ \int g(X_ {n,1},\ldots,X_ {n,(d-1)}\cdot X_ {n,(d+1)},\ldots, X_ {n,D})\,du}\]

は，他のすべての次元が与えられたときの d 番目の次元の条件付き分布である。

形式的には

\[\alpha\sim_{d}\beta \Leftrightarrow \alpha_ {i}=\beta_ {i}\hspace{1cm}\forall i\ne d\]

とすると、遷移確率は次のように書ける

\[\kappa(\alpha,\beta)= \left\{\begin{aligned} \frac{1}{D} \frac{g(\beta)}{\int_ {\gamma\sim_ {d}\alpha} g(\gamma)d\gamma} & \hspace{1cm}\text{ if }\beta\sim_ {d}\alpha\\ 0 & \hspace{1cm}\text{ otherwise}\\ \end{aligned}\right. \hspace{1cm}\forall \beta\ne\alpha\]

で期待通りの局所的なバランスが検証され，唯一の非自明なケースとなった。

\[g(\alpha)\kappa(\alpha,\beta) = \frac{1}{D}\frac{g(\alpha)g(\beta)}{\int_ {\gamma\sim_ {d}\alpha}g(\gamma)d\gamma} = \frac{1}{D}\frac{g(\beta)g(\alpha)}{\int_ {\gamma\sim_ {d}\beta}g(\gamma)d\gamma} = g(\beta)\kappa(\beta,\alpha)\]

3.5 メトロポリス・ヘイスティング遷移(∞)

ギブス法に関わる条件付き分布でさえ，あまりにも複雑で求めることができない場合がある。 そのような場合には，メトロポリス・ヘイスティングを利用することができる。 そのために，まず遷移を示唆する役割を果たす側面の遷移確率 $h(\cdot,\cdot)$ を定義する。 そして，反復 $n+1$ において，マルコフ連鎖が次に訪れるべき 状態を次のような過程で定義する。 まず，$h$ から「提案された遷移」$x$ を引き，それを受け入れる関連確率 $r$ を計算する。

\[x\sim h(X_ {n},\cdot)\hspace{1cm}\text{and}\hspace{1cm}r=\min\left(1,\frac{g(x)h(x,X_ {n})}{g(X_ {n})h(X_ {n},x)}\right)\]

そして、有効な遷移は以下のように選択される:

\[X_ {n+1}=\left\{ \begin{aligned} x & \hspace{1cm}\text{ with probability } r\\ X_ {n} & \hspace{1cm}\text{ with probability } 1-r\\ \end{aligned}\right.\]

形式的には，遷移確率は以下のように書くことができる:

\[\kappa(\alpha,\beta)= h(\alpha,\beta)\min\left(1,\frac{g(\beta)h(\beta,\alpha)}{g(\alpha)h(\alpha,\beta)}\right)\hspace{1cm}\forall\beta\ne\alpha\]

ということで，予想通りローカルバランスが検証された。

\[\begin{aligned} g(\alpha)\kappa(\alpha,\beta) &= g(\alpha)h(\alpha,\beta)\min\left(1,\frac{g(\beta)h(\beta,\alpha)}{g(\alpha)h(\alpha,\beta)}\right)=\min(g(\alpha)h(\alpha,\beta),g(\beta)h(\beta,\alpha))\\ &= g(\alpha)h(\alpha,\beta)\min\left(1,\frac{g(\beta)h(\beta,\alpha)}{g(\alpha)h(\alpha,\beta)}\right)=g(\beta)\kappa(\beta,\alpha)\\ \end{aligned}\]

3.6 サンプリング過程

マルコフ連鎖が定義できたら，ランダムな状態列 (ランダムに初期化) をシミュレートし，そのうちのいくつかは，目標とする分布に従うと同時に独立であるサンプルを得るように選択し続けることができる。

まず，狙った分布に (ほぼ) 従うサンプルを得るためには，マルコフ連鎖の定常状態 (定常状態は理論的には漸近的にしか到達しない) にほぼ到達するような生成系列の先頭から十分遠い状態のみを考慮する必要がある。 したがって，最初にシミュレートされた状態はサンプルとして使用できず，定常状態に到達するために必要なこの段階をバーンイン時間と呼ぶ。 実際には，このバーンイン時間の長さを知ることはかなり困難であることに注意。

次に (ほぼ) 独立なサンプルを得るためには，バーンイン時間後の系列の連続した状態を全て保持することはできない。 実際，マルコフ連鎖の定義では，2 つの連続した状態の間に強い相関があることを意味しており，ほぼ独立とみなせるほど互いに離れている状態のみをサンプルとして保持する必要がある。 実際には，ほぼ独立とみなされるために 2 つの状態の間に必要なラグは，自己相関関数の分析によって推定することができる (数値の場合のみ)。

そこで，目標とする分布に従う独立なサンプルを得るために，生成された系列から，互いにラグ L だけ離れていて，バーンイン時間 B の後に来る状態を保持することにする。 従って，マルコフ連鎖の連続する状態を

\[(X_ {n})_ {n\ge0}= X_ {0},X_ {1}, X_ {2},\ldots\]

のみをサンプルとする。

\[X_ {B}, X_ {B+L}, X_ {B+2L}, X_ {B+3L},\ldots\]

図 5. MCMC サンプリングではバーンイン時間とラグを考慮する必要がある。

4. 変分推論 (VI)

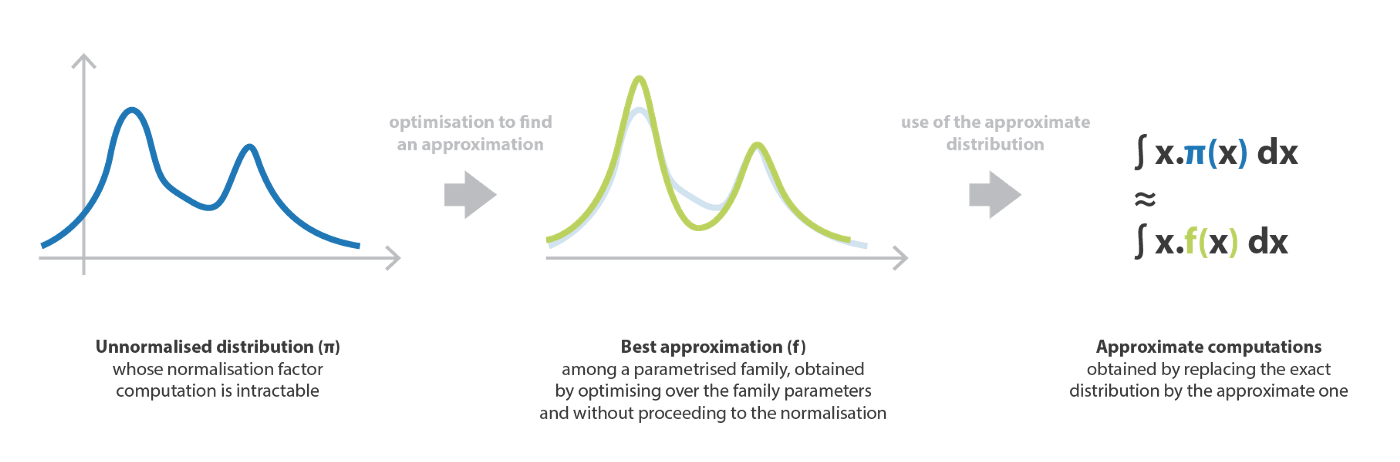
推論問題に関連する計算の難しさを克服するもう一つの可能な方法は，パラメター化された族の中から分布の最良の近似を見つけることからなる変分推論法を用いることである。 この最良の近似を見つけるために，我々は (族のパラメータに対する) 最適化処理に従う。

4.1 近似アプローチ

VI 法は，ある複雑な目標確率分布の最良の近似を，与えられた族の中から探索することからなる。 具体的には，パラメータ化された分布族を定義し，パラメータ上で最適化し，よく定義された誤差尺度に関して，目標に最も近い要素を得るというものである。

ここでまだ，正規化因子 C までで定義された確率分布 $\pi$ を考える。

\[\pi(\cdot)=C\times g(\cdot)\propto g(\cdot)\]

そして，より数学的に，パラメトリックな分布の族を表すと，以下のようになる:

\[\mathcal{F}_ {\Omega} = \left\{f_ {\omega};\omega\in\Omega\right\}\hspace{2cm}\Omega\equiv\text{ set possible parameters}\]

とし，2 つの分布 $p$ と $q$ の間の誤差尺度 $E(p,q)$ を考え，次のような最適なパラメータを探索する。

\[\omega^ {\star}=\text{argmin}_ {\omega\in\Omega} E(f_ {\omega},\pi)\]

もし $\pi$ を明示的に正規化することなくこの最小化問題を解くことができれば，難解な計算を扱う代わりに，$f_ {\omega}^ {\star}$ を近似値として用いて様々な量を推定することができるようになる。 変分推論が意味する最適化問題は，直接の計算 (正規化，組合せ論,…) よりはるかに単純に扱えるはずである。

サンプリングアプローチとは異なり，モデル (パラメトリック族) が仮定されるため，バイアスがかかるが分散も小さくなる。 一般に VI 法は MCMC 法より精度が劣るが，より速く結果が得られる。 これらの方法は，大規模で非常に統計的な問題によりよく適応している。


図 6. 近似アプローチ (変分推論) の説明図

4.2 分布族

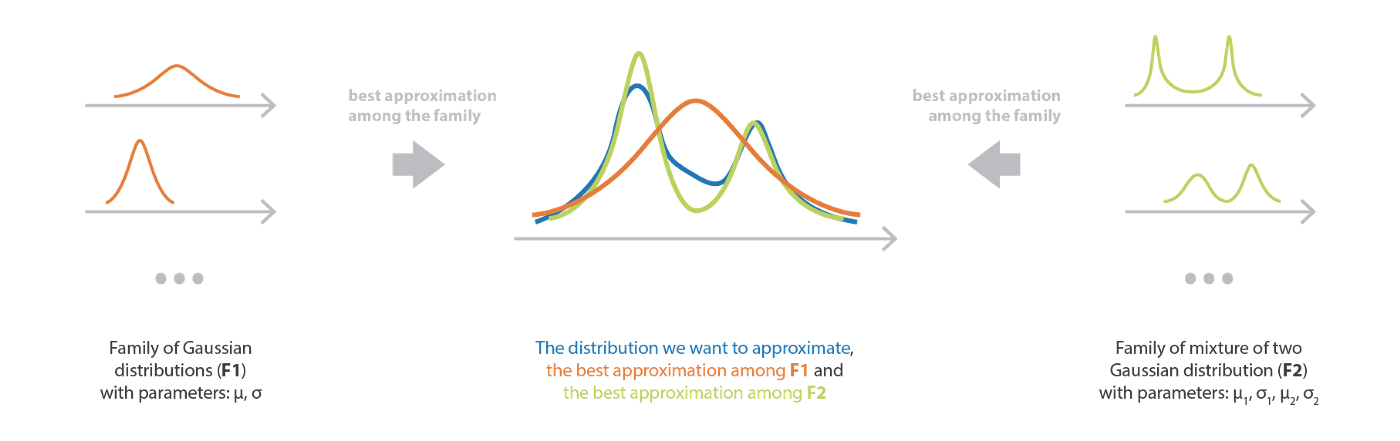
最初に設定する必要があるのは，最良の近似を探索する空間を定義するパラメータ化された分布族である。

族を選択することで，手法の偏りと複雑さの両方を制御するモデルが定義される。 かなり限定的なモデル (単純族) を仮定すると，バイアスは高くなるが，最適化処理は単純になる。 逆に，かなり自由なモデル (複雑な族) を仮定すると，バイアスはかなり低くなるが，最適化は難しくなります (難解ではないにしても)。 このように，最終的な近似の品質を保証するのに十分な複雑な族と，最適化処理を扱いやすくするのに十分な単純な族の間の適切なバランスを見出す必要がある。 もし，族内のどの分布も目標分布に近くない場合は，最良の近似であっても悪い結果になることを心に留めておく必要がある。

平均場変分族 は，考慮されたランダムベクトルのすべての成分が独立である確率分布族である。 この系列の分布は，各独立成分が積の異なる因子によって支配されるような積密度を持つ。 したがって，平均場変分族に属する分布は，次のように書くことができる密度を持つ。

\[f(z)=\prod_ {j=1}^ {m}f_ {j}(z_ {j})\]

ここで $m$ 次元の確率変数 $z$ を仮定している。 表記が省略されていても，すべての密度 $f_ {j}$ はパラメータ化されていることに注意。 例えば，各密度 $f_ {j}$ が平均と分散のパラメータを持つ正規分布である場合，大域的密度 $f$ はすべての独立した要因から来るパラメータのセットによって定義され，最適化はこのパラメータのセット全体に対して行わる。


図 7. 変分推論における分布族の選択は，最適化処理過程の難易度と最終的な近似の質の両方を設定する

4.3 カルバック・ライブラー・ダイバージェンス

分布族が定義されれば，与えられた確率分布 (正規化因子まで明示的に定義されている) の最良の近似を，この分布族の中からどのように見つけるか，という問題である。 最良近似は明らかに我々が考慮する誤差測定の性質に依存するとしても，我々が比較したいのは量そのものよりも量分布 (確率分布としてはユニタリーでなければならない) なので、最小化問題は正規化因子に敏感であってはならないと考えるのは極めて自然だと思われる。

そこで，カルバック・ライブラー (KL) ダイバージェンスを定義し，この尺度が問題を正規化要因に左右されなくすることを見てみよう。 $p$ と $q$ を 2 つの分布とすると，KL ダイバージェンスは以下のように定義される:

\[KL(p,q)=\mathbb{E}_ {z\sim p}\left[\log p(z)\right] - \mathbb{E}_ {z\sim p}\left[\log q(z)\right]\]

この定義により，容易に以下を得る:

\[KL(f_ {\omega}, C_ {g})=\mathbb{E}_ {z\sim f_ {\omega}}\left[\log f_ {\omega}(z)\right]-\mathbb{E}_ {z\sim f_ {\omega}}\left[\log(C_ {g}(z))\right] = \mathbb{E}_ {z\sim f_ {\omega}}\left[\log f_ {\omega}(z)\right]-\mathbb{E}_ {z\sim f_ {\omega}}\left[\log g(z)\right] -\log C.\]

これは最小化問題に対して以下の等式を意味する。

\[\omega^ {\star}=\text{arg min}_ {\omega\in\Omega}\text{KL}(f_ {\omega},\pi)=\text{arg min}_ {\omega\in\Omega}\text{KL}(f_ {\omega}, C_ {g}) = \text{arg min}_ {\omega\in\Omega}\text{KL}(f_ {\omega}, g)\]

このように，誤差指標として KL ダイバージェンスを選択した場合，最適化処理は乗法係数に影響されず，予想されたように，対象となる分布の苦しい正規化因子を計算することなく，パラメトリックな分布群の中から最良の近似値を探索することができる。

最後に，副次的な事実として KL ダイバージェンスは交差エントロピーからエントロピーを引いたものであり，情報理論において素晴らしい解釈を持っていることに注目して，本節を締めくくる。

4.4 最適化処理と直観的な理解

パラメトリック族と誤差測定の両方が定義されると，パラメータを初期化し (ランダムに，または明確に定義された戦略に従って)，最適化に進むことができる。 勾配降下や座標降下など，いくつかの古典的な最適化手法を用いることができ，実際には局所的な最適値に到達することになる。

この最適化過程をよりよく理解するために，ベイズ推定問題の具体的なケースに戻り，次のような事後分布を仮定する。

\[p(z\vert x)\propto p(x\vert z)p(z) = p(x,z)\]

この場合，変分推論を用いてこの事後推定値の近似値を得ようとすると，以下の最適化過程を解く必要がある (パラメター化された族が定義され，誤差指標として KLダイバージェンスを仮定する場合)。

\[\begin{aligned} \omega^ {\star} &=\text{argmin}_ {\omega\in\Omega} \text{KL}(f_ {\omega}(z), p(z\vert x))\\ &=\text{argmin}_ {\omega\in\Omega} \text{KL}(f_ {\omega}(z), p(x,z))\\ &=\text{argmax}_ {\omega\in\Omega} \left(-\text{KL}(f_ {\omega}(z), p(x,z)\right)\\ &=\text{argmax}_ {\omega\in\Omega}\left(\mathbb{E}_ {z\sim f_ {\omega}}\left[\log p(z)\right] + \mathbb{E}_ {z\sim f_ {\omega}}\left[\log p(x\vert z) \right] - \mathbb{E}_ {z\sim f_ {\omega}}\left[\log f_ {\omega}(z)\right]\right)\\ &=\text{argmax}_ {\omega\in\Omega} \left(\mathbb{E}_ {z\sim f_ {\omega}}\left[\log p(x\vert z)\right]- \text{KL}(f_ {\omega},p(z))\right)\\ \end{aligned}\]

最後の等式は，近似値がどのようにその量を分配するように促されるかをよりよく理解するのに役立つ。 最初の項は，期待対数尤度で，観測されたデータを最もよく説明する潜在変数 $z$ の値に近似の量を配置するようにパラメータを調整する傾向がある。 第 2 項は，近似と事前分布の間の負の KL ダイバージェンスであり，近似を事前分布に近づけるためにパラメータを調整する傾向がある。 したがって，この目的関数は，通常の事前分布と尤度のバランスをよく表している。


図 8. 変分推論アプローチの最適化過程

5. お持ち帰り

この記事の主な点，以下の通り:

  • ベイズ推定は統計学や機械学習におけるかなり古典的な問題で，よく知られたベイズの定理に依存している。その主な欠点は，ほとんどの場合，いくつかの非常に重い計算である。
  • マルコフ連鎖モンテカルロ法 (MCMC) は，非常に複雑な密度や，ある係数まで定義された密度からサンプルをシミュレートすることを目的としている。
  • MCMC は，ベイズ推定において，難解な計算を扱う代わりに，事後的に「正規化されていない部分」から直接，作業するためのサンプルを生成するために使用することができる。
  • 変分推論 (VI) は分布を近似するための手法で，パラメータに対する最適化処理を用いて，与えられた族の中から最良の近似を見つける。
  • VI 最適化処理は対象分布の乗法定数に影響されないので，ある正規化係数までしか定義されていない事後分布を近似するのに使用できる。

すでに述べたように，MCMC 法と VI 法は異なる特性を持っており，それは異なる典型的な使用例を意味する。 一方では MCMC アプローチのサンプリング処理はかなり重いが，バイアスがないので，正確な結果を期待する場合には，時間を気にせずこれらの方法が好まれる。 一方 VI 法における族の選択は，明らかにバイアスをもたらす。だが，合理的な最適化処理を伴うので，これらの方法は，高速計算を必要とする非常に大規模な推論問題に特に適応している。

MCMC と VI とのその他の比較は，変分推論: 統計学者のためのレビュー 論文に記載されている。 VI にしか興味がない読者には強くお勧めする。 MCMC についての詳しい情報は，この一般的な紹介論文 と，機械学習指向の紹介論文 をお勧めする。 LDA に適用される Gibbs サンプリングについてもっと知りたい方は，Tutorial on Topic Modelling and Gibbs Sampling を参照 (LDA Gibbs Sampler についての講義ノート と合わせて，慎重に導出することができる)。

最後に，少しおちゃらけて，次回の記事で変分推論に基づく深層学習のアプローチである変分自己符号化器について述べることにしましょう。 それではご期待ください。

読んでくださってありがとうございます！もしあなたがそれに値すると思ったら、お気軽にシェアしてください。