Understanding Variational Autoencoders (VAEs)
変分自己符号化器 (VAE:Variational Auto Encoders) の理解
VAE の理解へ導くステップ・バイ・ステップでの構築
- Joseph Rocca

- 原著
- 本記事は Baptiste Rocca との共著
1. はじめに
ここ数年,深層学習をベースにした生成モデルは,この分野における驚くべき進歩により,ますます注目を集めている。 この分野では,驚くべき進歩を遂げている。 膨大な量のデータ,適切に設計されたネットワークアーキテクチャ,そしてスマートな学習技術を利用して,深層生成モデルは,画像,テキスト,音声などの様々な種類のコンテンツを非常にリアルに生成する驚くべき能力を示している。 これらの深層生成モデルの中でも,特に注目すべき 2 つの主要なファミリーがあり,特別な注意を払う必要がある。 それらは GAN(Generative Adversarial Networks)とVAE(Variational Autoencoders)である。

今年の 1 月に公開した前回の記事では Generative Adversarial Networks (GANs) について詳しく説明し,特に,敵対的な学習によって,生成器と識別器という 2 つのネットワークを対立させ,反復に次ぐ反復で両方を改善させる方法を紹介しました。 この記事では,もう 1 つの主要な深層生成モデルを紹介する。 Variational Autoencoders (VAE) である。 一言で言えば VAE とは,学習中に符号化器分布が正則化され,潜在空間が新しいデータを生成するのに適した特性を持つことを保証する自己符号化器のことである。 また 変分 (variational) という言葉は,正則化と統計学における変分推論法との間に密接な関係があることに由来している。
最後の 2 つの文章が VAE の概念をよく表しているとすれば,それは多くの疑問を投げかけるものでもあろう。 自己符号化器とは何か? 潜在空間とは何か,なぜそれを正則化するのか? VAE から新しいデータを生成する方法は? VAE と変分推論の間にはどのようなつながりがあるのか? VAE を可能な限り説明するために,これらすべての質問 (そして他の多くの質問も!) に答え,できる限り多くの洞察 (基本的な直観からより高度な数学的詳細まで) を読者に提供しよう。 したがって,この記事の目的は,変分自己符号化器が依拠している基本的な概念を議論するだけでなく,これらの概念につながる推論を最初から段階的に構築することにある。
それでは,一緒に VAE を(再)発見しよう!
1.1 概要
第 1 節では,VAE の理解に役立つ次元削減と自己符号化器に関するいくつかの重要な概念を確認する。 次に第 2 節では,自己符号化器が新しいデータの生成に使用できない理由を示し,生成過程を可能にする自己符号化器の正則化版である変分自己符号化器を紹介する。 最後に,変分推論に基づいて VAE をより数学的に説明する。
2. 次元削減,PCA,自己符号化器
この最初の節では,次元削減に関連するいくつかの概念について説明することから始める。 特に,主成分分析 (PCA) と自己符号化器について簡単に概説し,両者の考え方がどのように関連しているかを説明する。
2.1 次元削減とは?
機械学習において 次元削減 とは,あるデータを記述する特徴の数を減らす処理のことである。 次元削減は,選択 (既存のいくつかの特徴のみを保存する) または抽出 (古い特徴を基に新しい特徴の数を減らす) により行われ,低次元のデータを必要とする多くの状況 (データの可視化,データストレージ,重い計算…) で有用である。 次元削減には様々な手法があるが,これらの手法のほとんどに適合する大域的な枠組みを設定することができる (ないとしても!)。
まず「古い特徴」表現から「新しい特徴」表現を (選択または抽出によって) 生成する処理を 符号化器,その逆を 復号化器 と呼ぶことにする。 次元削減は,符号化器がデータを圧縮し (初期空間から符号化空間へ),復号化器がデータを伸長するデータ圧縮と解釈することができる。 もちろん,初期データ分布,潜在空間次元,符号化器の定義によっては,この圧縮は非可逆的であり,符号化中に情報の一部が失われ,復号時に復元できないことを意味する。
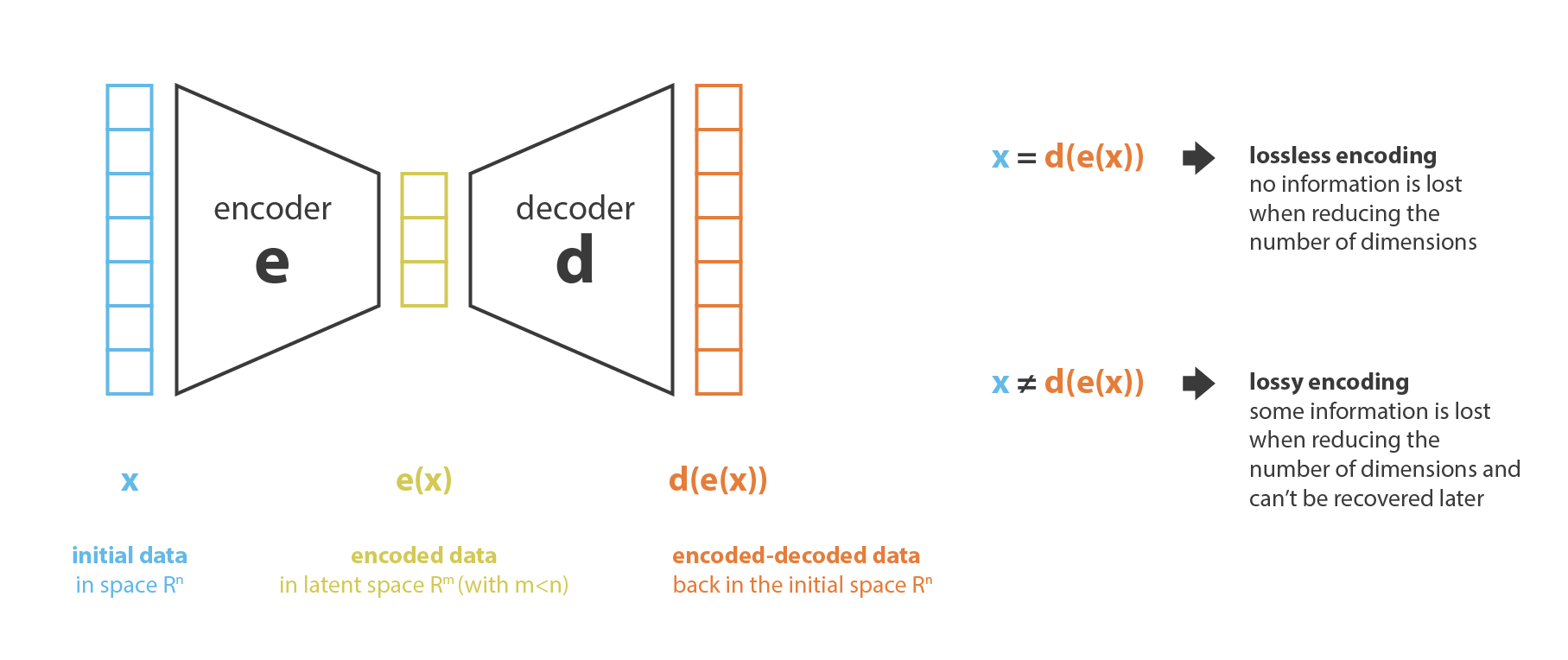
次元削減法の主な目的は,与えられたファミリーの中から最適な符号化/復号化の対を見つけることである。 言い換えれば,与えられた符号化と復号化のセットに対して,符号化時に最大限の情報を保持し,復号化時に最小限の再構成誤差を持つ対を探すことである。 符号化器と復号化器のファミリーをそれぞれ $E$ と $D$ とすると,次元削減問題は次のように書くことができる。 (訳注: エンコーダ $E$ とデコーダ $D$ だが,Kingma and Welling (2014) の原著論文では $q_{\phi}(x)$ と $p_{\theta}(z)$ と表現している。)
\((e^{* },d^{* })=\arg\min_{(e,d)\in E\times D} \epsilon\left(x,d(e(x))\right),\) ここで $e(x,d(e(x)))$ は,入力データ $x$ と符号化・復号化データ $d(e(x))$ との間の再構成誤差を定義する。 最後に,以下では $N$ をデータ数,$n_ {d}$ を初期 (復号化) 空間の次元,$n_ {e}$ を縮減 (符号化) 空間の次元とする。
2.2 主成分分析(PCA)
次元削減といえば,まず思い浮かぶのが 主成分分析 (PCA) である。 PCA が今説明した枠組みにどのように適合するかを示し,自己符号化器へのリンクを作るために,PCA がどのように機能するかについて,ほとんどの詳細はさておき,非常に高い概要を説明する (このテーマについて完全な記事を書く予定があることに注意)。
PCA の考え方は,$n_ {d}$ 個の古い特徴の 線形結合 である $n_ {e}$ 個の新しい 独立した 特徴を構築し,これらの新しい特徴によって定義される部分空間へのデータの投影が初期データにできるだけ近くなるようにすることである (ユークリッド距離の意味で)。 言い換えれば PCA は (新しい特徴の直交基底によって記述される) 初期空間の最良の線形部分空間を探しており,この部分空間への投影によってデータを近似する際の誤差が可能な限り小さくなるようにする。
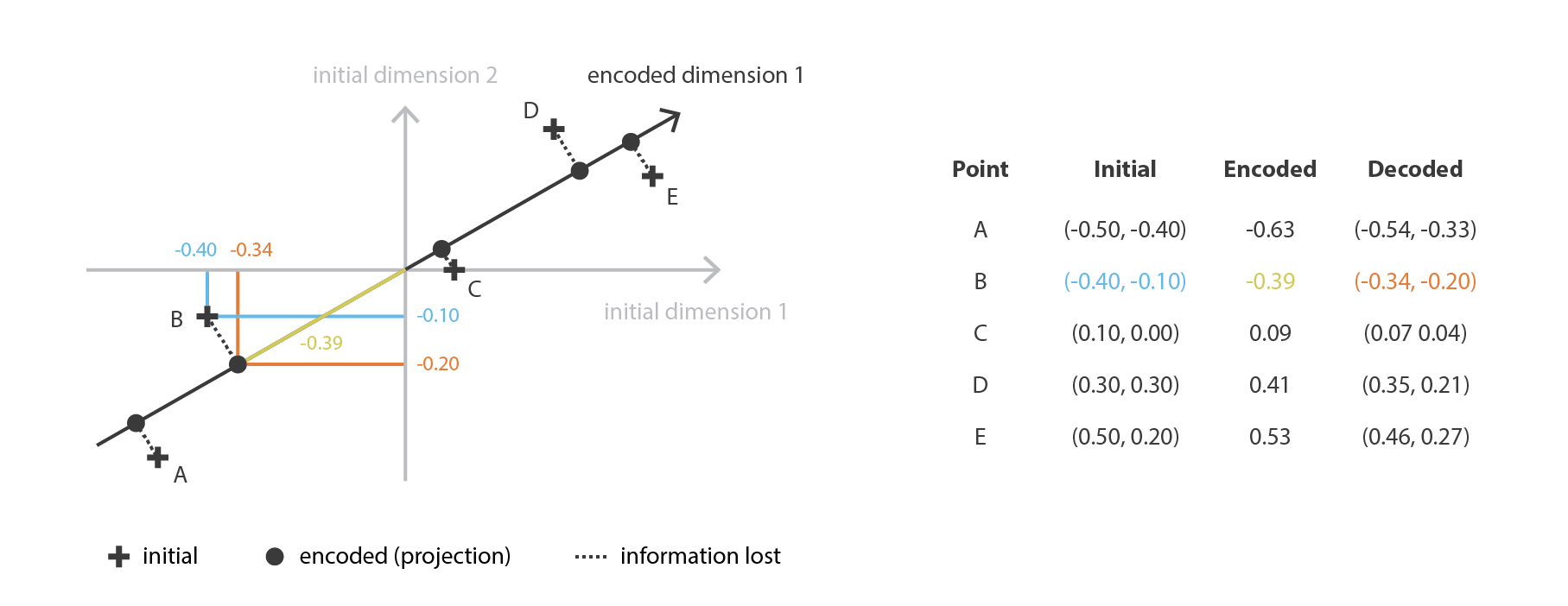
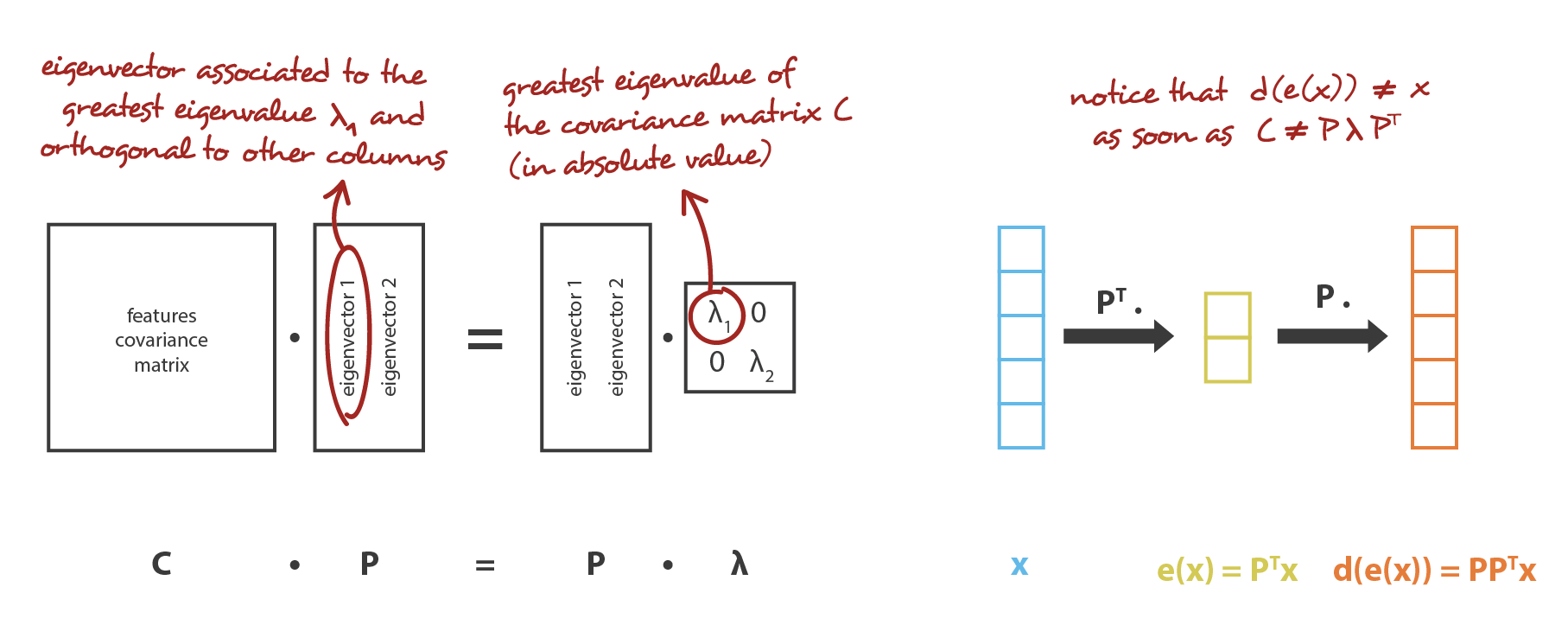
我々の大域的枠組みに置き換えると,行が正規直交する $n_ {e}\times n_ {d}$ 行列 (線形変換) の族 $E$ に符号化を,$n_ {d} \times n_ {e}$ 行列の族 $\mathcal{D}$ に復号化器を探すことになる。 共分散特徴行列の (ノルムの) 最大固有値 $n_ {e}$ に対応するユニタリー固有ベクトルは直交しており (あるいはそうなるように選択できる),近似誤差を最小にしてデータを投影するための次元 $n_ {e}$ の最適部分空間を定めることが示されている。 したがって,これらの $n_ {e}$ 個の固有ベクトルを新しい特徴として選択することができ,次元削減の問題は固有値/固有ベクトル問題として表現することができる。 さらに,このような場合,復号化行列は符号化行列の転置行列であることも示すことができる。
2.3 自己符号化器
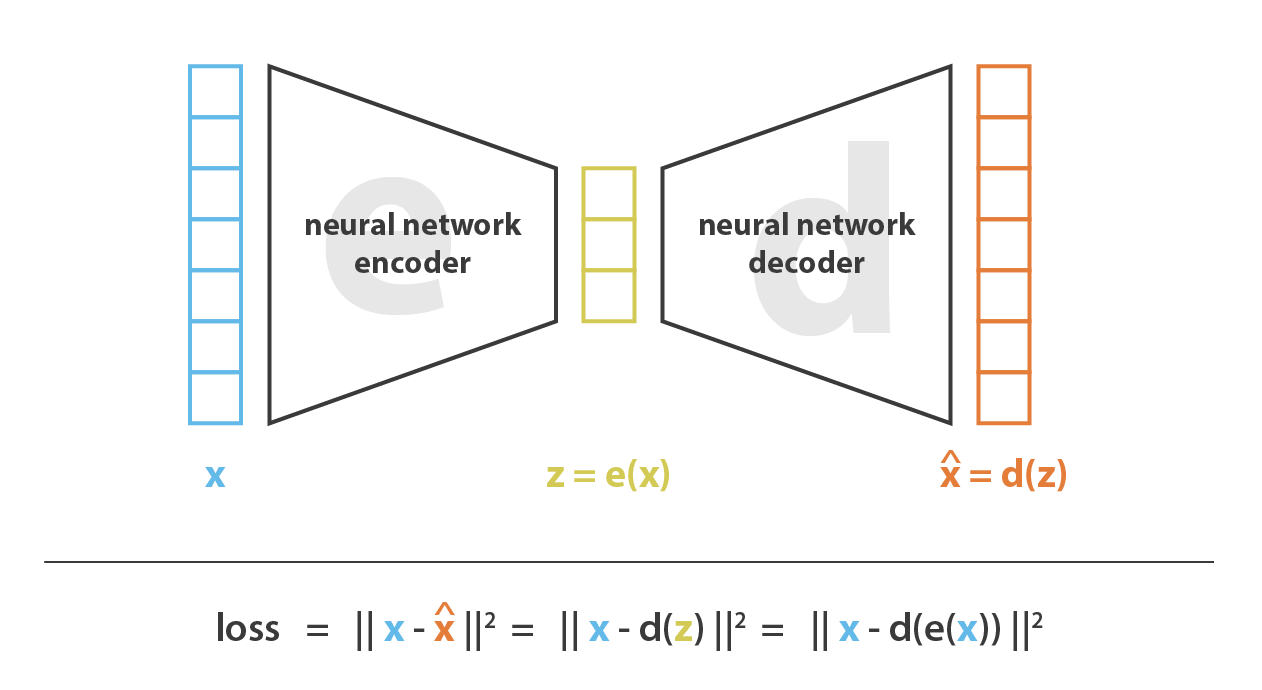
ここで 自己符号化器 について説明し,ニューラルネットワークをどのように次元削減に利用できるかを見る。 自己符合器は,符号化器と復号化器をニューラルネットワークとして設定し,最適な符号化・復号化方式を繰り返し学習させるという,非常に簡潔な考え方である。 すなわち,各反復計算において,自己符号化器アーキテクチャ (符号化器と復号化器) にいくつかのデータを与え,符号化-復号化出力を初期データと比較し,その誤差をアーキテクチャを通してバックプロパゲートし,ネットワークの重みを更新する。
このように,直感的には,自己符号化器アーキテクチャ全体 (符号化器+復号化器) がデータに対してボトルネックを作り,情報の主要な構造部分のみを通過させ,再構築することを保証している。 我々の一般的な枠組みを見ると,考慮される符号化器のファミリー E は符号化器ネットワークアーキテクチャによって定義され,考慮される復号化器のファミリー D は復号化ネットワークアーキテクチャによって定義され,再構成誤差を最小化する符号化と復号化の探索はこれらのネットワークのパラメータに対する勾配降下によって行われる。
まず,我々の符号化器と復号化器の両方のアーキテクチャが,非線形性を持たない 1 層だけのもの (線形自己符号化器) であると仮定する。 このような符号化器と復号化器は,行列で表現できる単純な線形変換である。 このような状況では PCA と同じように,データを投影する際にできるだけ情報の損失が少ない最適な線形部分空間を探すという意味で,PCA との明確な関連性を見出すことができる。 PCA で得られた符号化および復号化行列は,当然,勾配降下法で到達して満足する解の 1 つを定義するが,これが唯一のものではないことを概説しておく。 実際 複数の基底が同じ最適部分空間 を記述するように選ぶことができ,したがって,いくつかの符号化器/復号化器の対が最適な再構成誤差を与えることができる。 さらに,線形自己符号化器では,PCA とは逆に,最終的に得られる新しい特徴は独立である必要はない (ニューラルネットワークでは直交性の制約はない)。
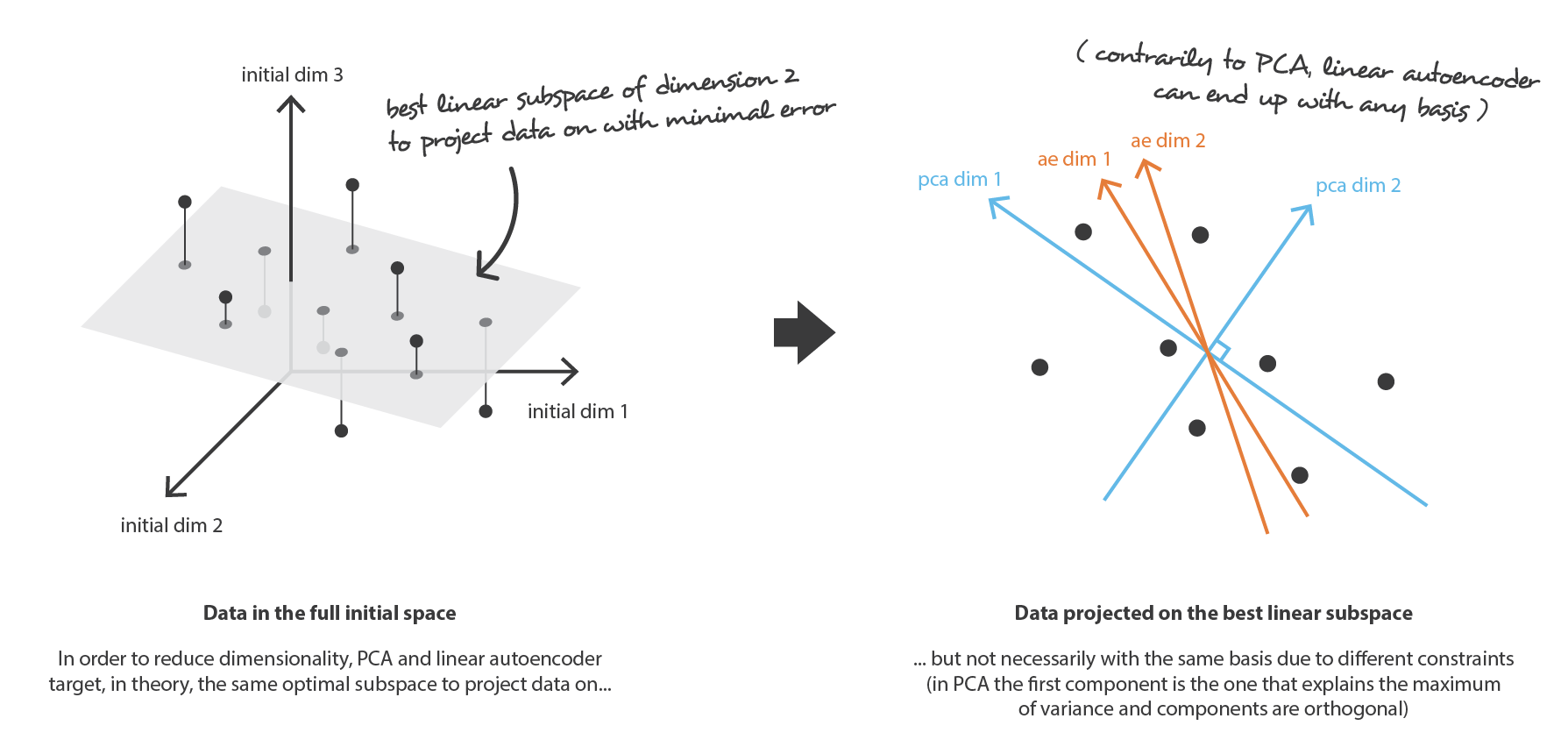
ここで,符号化器と復号化器の両方が多層で,かつ非線形であると仮定しよう。 このような場合,アーキテクチャが複雑であればあるほど,自己符号化器は再構成損失を低く抑えながら高次元縮小を進めることができる。 直感的には,符号化器と復号化器に十分な自由度があれば,どんな初期次元数でも 1 にすることができる。 実際「無限の力」を持つ自己符号化器は,理論的には N 個の初期データ点を受け取り,それらを $1, 2, 3, \ldots, N$ 個まで (より一般的には実軸上の N 個の整数として) 符号化し,関連する復号化器はその過程で損失なしに逆変換を行うことが可能である。
ただし,ここで 2 つのことを念頭に置く必要がある。 第 1 に,再構成の損失を伴わない重要な次元削減は,しばしば,潜在空間における解釈可能で利用可能な構造の欠如 (規則性の欠如) という代償を伴う。 第 2 に,ほとんどの場合,次元削減の最終目的は,データの次元数を減らすことだけではなく,データ構造情報の大部分を削減後の表現に残したまま,この次元数を減らすことである。 この 2 つの理由から,潜在空間の次元と自己符号化器の「深さ」 (圧縮の程度と品質を定義する) は,次元削減の最終目的に応じて慎重に制御・調整されなければならない。

3. 変分自己符号化器
これまで,次元削減問題を取り上げ,勾配降下法で学習可能な符号化・復号化のアーキテクチャである自己符号化器を紹介してきた。 ここで,コンテンツ生成問題とリンクさせ,この問題に対する現在の自己符号化器の限界を見て,変分自己符号化器を紹介する。
3.1 コンテンツ生成のための自己符号化器の限界
ここで「自己符号化器とコンテンツ生成の関係はどうなっているのか」という疑問が自然に湧いてくる。 確かに,自己符号化器が学習されると,符号化器と復号化器の両方が手に入るが,新しいコンテンツを生成する真の方法はまだない。 一見すると,潜在空間が十分に規則的であれば (学習過程で符号化器がよく「体制化して整理」した),その潜在空間からランダムに点を取って復号化すれば新しいコンテンツが得られると考えたくなる。 復号化器 は 生成敵対ネットワーク GAN の生成器のような働きをする。
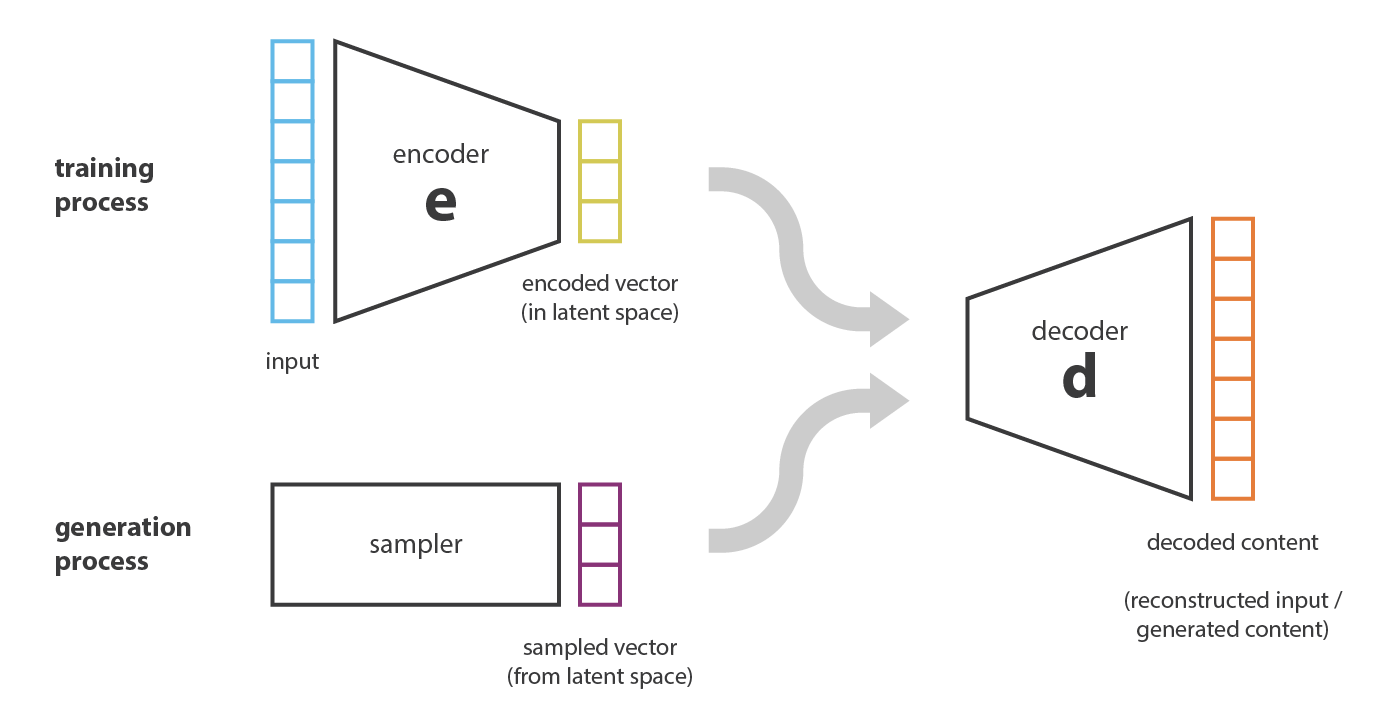
しかし,前節で述べたように,自己符号化器の潜在空間の規則性は,初期空間におけるデータの分布,潜在空間の次元,符号化器のアーキテクチャに依存する難しい点である。 従って,先験的に,符号化器が先程説明した生成過程に適合したスマートな方法で潜在空間を整理することを保証することは (不可能ではないにしても) かなり困難である。
この点を説明するために,前に述べた,任意の N 個の初期学習データを実軸上に置き (各データ点は実数値として符号化される),それを再構成損失なしに復号するのに十分強力な符号化器と復号化器を説明する例を考える。 このような場合,(潜在空間の次元が低いにもかかわらず) 情報損失を伴わない符号化・復号化を可能にする自己符号化器の高い自由度は,潜在空間のいくつかの点が復号されると無意味な内容を与えることを意味する厳しい オーバーフィッティング につながる。 この 1 次元の例が極端な例として選ばれたのであれば,自己符号化器の潜在空間の規則性の問題はもっと一般的であり,特別な注意を払うべきものであることに気づく。

少し考えてみると,潜在空間に符号化されたデータに構造がないのは,ごく当たり前のことである。 実際,自己符号化器が学習する課題の中には,このような組織を得ることを強制するものはない。 自己符号化器は,潜在空間がどのように構成されていても,できるだけ損失を少なくして符号化・復号化するようにしか訓練されていない。 したがって,アーキテクチャの定義に注意を払わないと,学習中にネットワークが過学習の可能性を利用して,できる限り課題を達成しようとするのは当然である。明示的に正則化しなければ。
3.2 変分自己符号化器の定義
そこで,自己符号化器の復号化器を生成目的に使用できるようにするために,潜在空間が十分に正則であることを確認する必要がある。 このような正則性を得るための一つの方法として,学習過程で明示的な正則化を導入することが考えられる。 したがって,この記事の冒頭で簡単に述べたように 変分自己符号化器とは,過学習を避け,潜在空間が生成処理を可能にする良い特性を持つことを保証するために学習が正則化された自己符号化器であると定義することができる。
変分自己符号化器は,標準的な自己符号化器と同様に,符号化器と復号化器からなるアーキテクチャであり,符号化・復号化されたデータと初期データ間の再構成誤差を最小化するように学習されるものである。 しかし,潜在空間に正則化を導入するために,符号化-復号化の処理を少し修正する。 入力を 1 つの点として符号化するのではなく,潜在空間上の分布として符号化する。 そして,モデルは以下のように学習される。
- 入力は潜在空間上の分布として符号化される
- 潜在的な空間から点がサンプリングされる
- サンプリングされた点は符号化され,再構成誤差を計算することができる
- 再構成誤差はネットワークを通じて逆伝播される

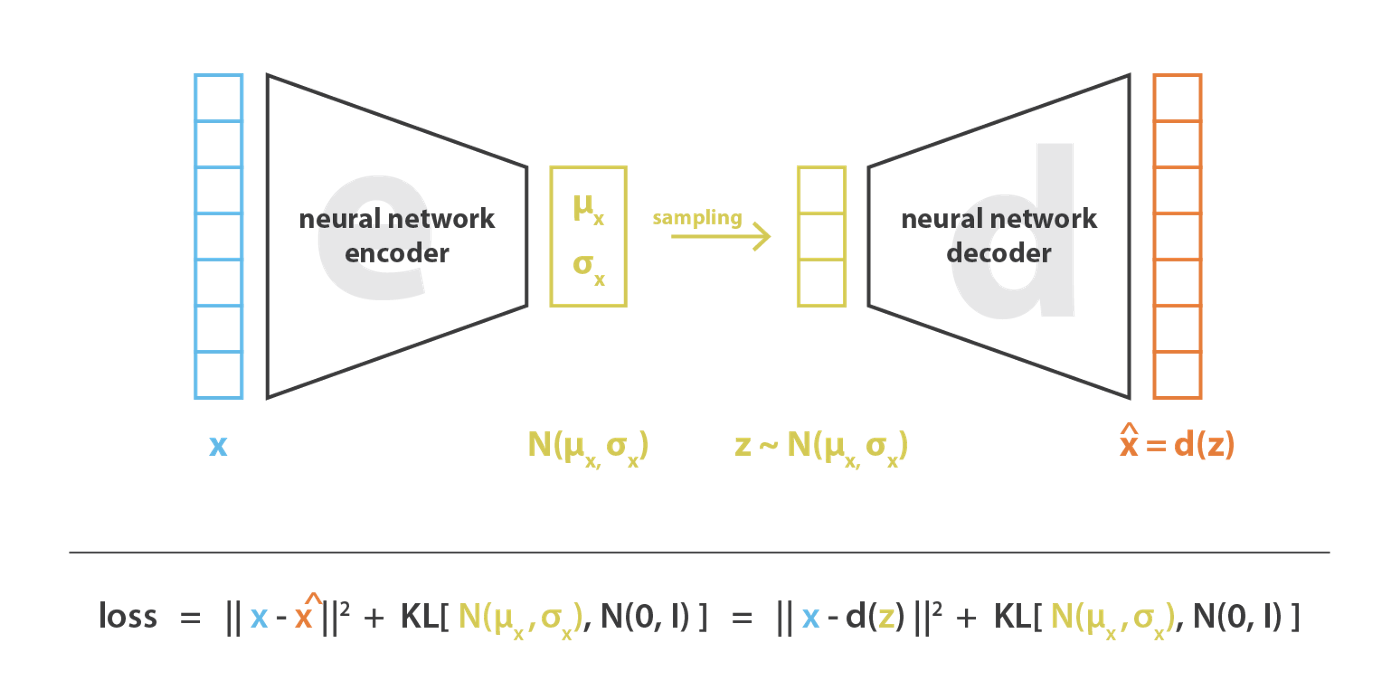
実際には,自己符号化器がガウス分布を記述する平均と共分散行列を返すように学習できるように,符号化された分布は正規分布に選ばれる。 入力が 1 点ではなく,ある分散を持つ分布として符号化される理由は,潜在空間正則化を非常に自然に表現することができる。 符号化器が返す分布は,標準正規分布に近くなるように強制される。 次節では,この方法で潜在空間の局所的および大域的正則化 (分散制御のため局所的に,平均制御のため大域的に) を保証することを見る。
したがって VAE を学習する際に最小化される損失関数は「再構成項」(最終層) と「正則化項」(潜在層) から構成され,それは符号化器によって返される分布を標準正規分布に近づけることによって潜在空間の組織を正則化する傾向がある。 この正則化項は、返された分布と標準ガウス分布の間の カルバック・ライブラー ダイバージェンス として表され,次節でさらに正当化される。 2 つのガウス分布の間のカルバック・ライブラーのダイバージェンスは,2 つの分布の平均と共分散行列で直接表現できる閉じた形式を持っていることに気がづく。
3.3 正則化に関する直感
生成過程を可能にするために潜在空間に期待される規則性は,主に 2 つの特性によって表現できる。 連続性 (潜在空間内の 2 つの近接した点は,一度復号されると全く異なる内容を与えてはならない) と 完全性 (選択された分布に対して潜在空間からサンプリングされた点は,一度復号されると「意味のある」内容を与えるべきである) である。

VAE は入力を単純な点ではなく,分布として符号化するという事実だけでは,連続性と完全性を確保するのに十分ではありません。 うまく定義された正則化項がないと,モデルは再構成誤差を最小にするために,分布が返されるという事実を「無視」して,ほとんど古典的な自己符号化器のように振る舞うことを学習することができる ( 過学習につながる)。 これを行うために,符号化器は小さな分散の分布を返すか (これは時間的分布になりがちである),非常に異なる平均の分布を返すか (これは潜在空間内で互いに本当に離れていることになる),のどちらかを行うことができる。 どちらの場合も,分布は間違った方法で使用され (期待された利益がキャンセルされ),連続性,完全性が満たされない。
そこで,これらの効果を避けるために,符号化器が返す分布の共分散行列と平均の両方を正則化する必要がある。 実際には,この正則化は,分布が標準正規分布に近くなるように強制することで行われる (中央化,縮小)。 この方法では,共分散行列が恒等式に近くなるように要求し,正確な分布を防ぎ,平均が 0 に近くなるように要求し,符号化された分布が互いに離れすぎないようにする。
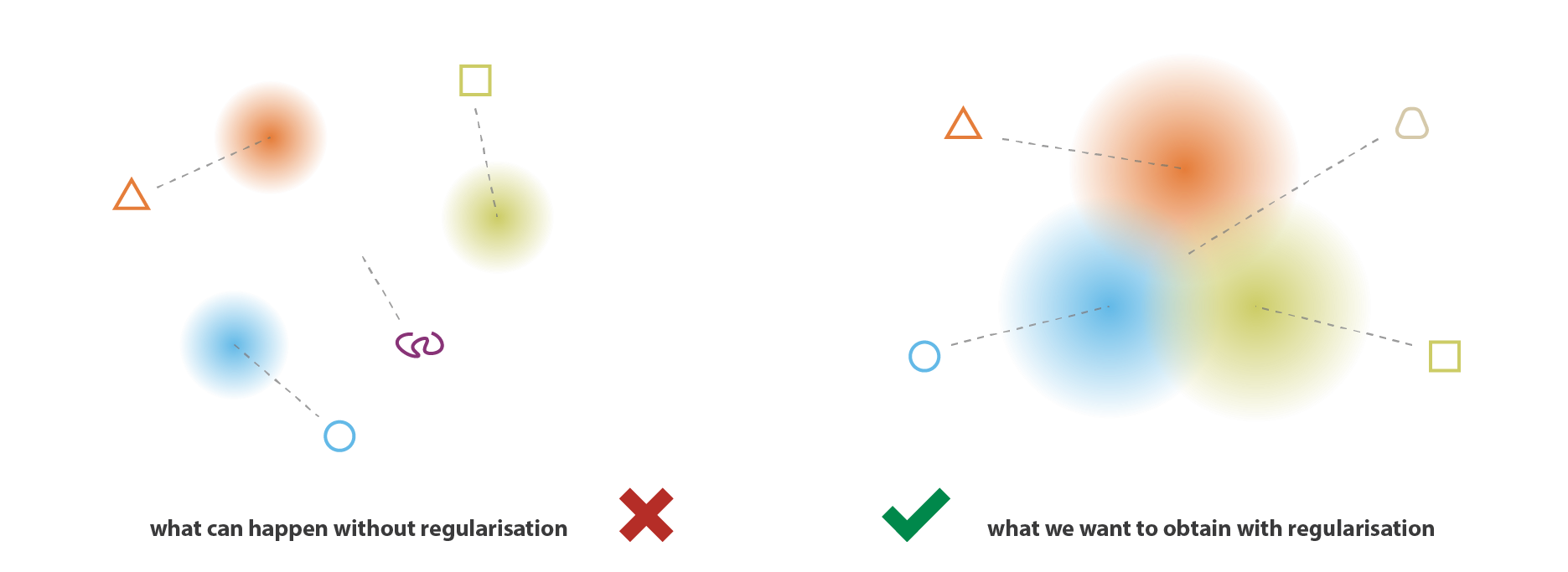
この正則化項により,モデルが潜在空間内の離れたデータを符号化するのを防ぎ,返された分布ができるだけ「重なる」ように促し,このようにして期待される連続性と完全性の条件を満足させることができる。 当然ながら,どの正則化項も,訓練データの再構成誤差を大きくする代償を払うことになる。 しかし,再構成誤差と KL ダイバージェンスのトレードオフは調整可能であり,次節では,そのバランスの表現が我々の公式導出からどのように自然に出てくるかを見ていく。
最後に,正則化によって得られる連続性と完全性は,潜在空間にコード化された情報に対して「勾配」を作る傾向 があることが分かる。 例えば,異なる学習データから得られた 2 つの符号化された分布の平均値の中間にある潜在空間の点は,最初の分布を与えたデータと 2 番目の分布を与えたデータの間のどこかにあるもので,両方のケースで自己符号化器によってサンプリングされるかもしれないので,復号化されるはずである。

4. VAEの数学的詳細
前節では、以下のような直感的な概要を説明した。 VAEは入力を点ではなく,分布としてエンコードするオートエンコーダであり,その潜在空間の「構造化」は符号化器が返す分布が標準正規分布に近くなるように制約することによって正則化される。 本節では,正則化項をより厳密に正当化することができるように,VAE のより数学的な見方を提供する。 そのために,明確な確率的枠組みを設定し,特に変分推論の技法を用いる。
4. 確率論的な枠組みと仮定
まず,データを記述するための確率的グラフィカルモデルを定義することから始める。 データを表す変数を $x$ とし,$x$ は直接観測されない潜在変数 $z$ (符号化された表現) から生成されると仮定する。 従って,各データ点に対して,以下の 2 段階の生成過程が想定される。
- 潜在表現 $z$ を事前分布 $p(z)$ からサンプリングする。
- データ $x$ を条件付き尤度分布$ p(x\vert z)$ からサンプリングする。
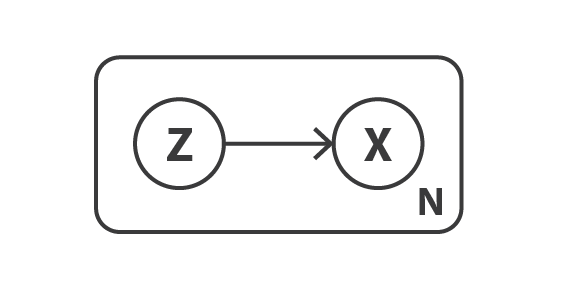
このような確率モデルを念頭に置くと,符号化器と復号化器の概念を再定義することができる。 実際,単純な自己符号化器が決定論的な符号化器と復号化器を考えるのとは対照的に, この 2 つの対象の確率論的バージョンを考える。 確率的符号化器は,符号化された変数の分布を表す $p(x\vert z)$ で定義され,確率論的符号化器は,符号化された変数の分布を表す $p(z\vert x)$ で定義される。
この時点ですでに,単純な自己符号化器では欠けていた潜在空間の正則化が,データ生成過程の定義に自然に現れている。 潜在空間における符号化された表現 $z$ は,事前分布 $p(z)$ に従うと仮定される。 事前分布 $p(z)$,尤度 $p(x\vert z)$,事後分布 $p(z\vert x)$ の間のリンクを作るよく知られたベイズの定理を使うことができる。
\(p(z\vert x)= \frac{p(x\vert z) p(z)}{p(x)} = \frac{p(x\vert z)p(z)}{\int p(x\vert u)p(u)du}\)
ここで $p(z)$ は標準正規分布であり,その平均は $z$ の変数の決定論的関数 $f$で定義される。 その共分散行列は恒等行列Iに乗ずる正の定数 $c$ の形をとる正規分布であると仮定する。 関数 $f$ は $F$ と呼ばれる関数族に属するものとし,この関数族は後で選択される。したがって,以下のようになる。
\(\begin{aligned} p(x) &\equiv \mathcal{N}(0,I)\\ p(x\vert z) &\equiv \mathcal{N}(f(z),cI)\hspace{2cm}f\in F, c>0\\ \end{aligned}\)
$f$ はよく定義され,固定されているとする。 理論的には $p(z)$ と $p(x\vert z)$ がわかっているので,ベイズの定理を使って $p(z\vert x)$ を計算することができる。 これは古典的な ベイズ推論問題 と呼ばれる。 しかし,前回の記事で述べたように,この種の計算は (分母に積分があるため) しばしば難解で,変分推論のような近似手法を用いる必要がある。
4.1 変分推論の定式化
統計学において、変動推論 (Variational Inference, VI) は複雑な分布を近似する手法の一つである。 そのアイデアは,パラメータ化された分布の族 (例えば,平均と共分散をパラメータとするガウス族) を設定し,この族の中から目的の分布の最良の近似を探すことである。 族内の最適な要素は,与えられた近似誤差 (ほとんどの場合,近似と目標間 のカルバック-ライブラーダイバージェンス) を最小化するもので,族を記述するパラメータに対する勾配降下法によって探索される。 詳細は 変分推論の投稿 とその中の参考文献を参照。
ここで,平均と共分散がパラメータ $x$ の 2 つの関数 $g$ と $h$ で定義される正規分布 $q_ {x}(z)$ で $p(z\vert x)$ を近似するとする。 この 2 つの関数は,それぞれ,後で指定する関数 G と H の族に属するが,パラメータ化されていることが前提である。 したがって,以下のように表すことができる。
\(q_{x}(z) \approx \mathcal{N}\left(g(x),h(x)\right)\hspace{1cm} g\in G, h\in H\)
そこで,このようにして変分推論の候補の族を定義し,関数 $g$ と $h$ (実際にはそのパラメータ) を最適化して,近似値と目標値 $p(z\vert x)$ の間のカルバック・ライブラー ダイバージェンス を最小にすることにより,この族から最良の近似値を見つける必要がある。 つまり,以下のような最適な $g^{\star }$ と $h^ {\star}$ を探す。
\(\begin{aligned} (g^{\star},h^{\star})&=\text{argmin}_{(g,h)\in G\times H} KL\left[q_{x}(z)||p(z|x)\right]\\ &= \text{argmin}_{(g,h)\in G\times H}\left(\mathbb{E}_{z\sim q_{x}}\left[\log q_{x}(z)\right] -\mathbb{E}_{z\sim q_{x}} \left[\log\left({p(x|z)p(z\over p(x)}\right)\right]\right)\\ &= \text{argmin}_{(g,h)\in G\times H}\left( \mathbb{E}_{z\sim q_{x}}\left[\log q_{x}(z)\right] -\mathbb{E}_{z\sim q_{x}} \left(\log p(z)\right) -\mathbb{E}_{z\sim q_{x}} \left(\log p(x|z)\right) -\mathbb{E}_{z\sim q_{x}} \left(\log p(x)\right) \right)\\ &= \text{argmin}_{(g,h)\in G\times H}\left( \mathbb{E}_{z\sim q_{x}}\left[\log p(x|z)\right] -KL\left[q_{x}(z)||p(z)\right] \right)\\ &= \text{argmin}_{(g,h)\in G\times H}\left( \mathbb{E}_{z\sim q_{x}}\left[ -{\left\|x-f(z)\right\|\over 2c} \right] -KL\left[q_{x}(z)||p(z)\right] \right)\\ \end{aligned}\)
最後から 2 番目の式では,事後分布 $p(z\vert x)$ を近似する際に「観測値」の尤度の最大化 (第 1 項の期待対数尤度の最大化) と事前分布に近づくこと (第 2 項の $q_ {x}(z)$ と $p(z)$ の間の KL ダイバージェンスの最小化) のトレードオフが存在することが観察される。 このトレードオフはベイズ推論問題では当然のことであり,データの信頼度と事前分布の信頼度の間で見出されるべきバランスを表現している。
これまで,我々は関数 $f$ が既知で固定であることを仮定し,その仮定下で変分推論技法を用いて事後分布 $p(z\vert x)$ を近似的に求めることができることを示してきた。 しかし,実際には,復号化器を定義するこの関数 $f$ は既知ではなく,また,選択する必要がある。 そのために,我々の当初の目標は,潜在空間が生成目的に使用できるほど正則な,性能の良い符号化・復号化方式を見つけることであった。 この規則性が潜在空間上で仮定される事前分布によって支配されている場合,符号化復号化スキーム全体の性能は関数 $f$ の選択に大きく依存する。 実際 $p(z\vert x)$ は $p(z)$ と $p(x\vert z)$ から (変分推論によって) 近似でき,$p(z)$ は単純な標準正規分布なので,我々のモデルで最適化を行うために自由に使えるのは,パラメータ $c$ (尤度の分散を定義する) と関数 $f$ (尤度の平均を定義する) の 2 つだけである。
そこで,先に説明したように $F$ の任意の関数 $f$ (それぞれ異なる確率的復号羽化器 $p(x\vert z)$ を定義) に対して $p(z\vert x)$ の最良近似 $q^ {\star }_ {x(z)}$ と表されるものが得られると考えることにする。 確率的な性質があるにもかかわらず,できるだけ効率的な符号化復号化方式を求め,そして $q^ {\star}_ {x(z)}$ から $z$ をサンプリングしたときに $z$ が与えられたときの期待対数尤度を最大化する関数 $f$ を選びたい。
換言すると,与えられた入力 $x$ に対して 分布 $q^ {\star }_ {x(z)}$ から $z$ を抽出し,分布 $p(x\vert z)$ から$\widehat{x}$ をサンプルしたときに $\hat{x}= x$とする確率を最大にしたい。したがって以下のような最適 $f^ {\star}$ を探している。 <!– So, let’s consider that, as we discussed earlier, we can get for any function $f$ in $F$ (each defining a different probabilistic decoder $p(x\vert z)$) the best approximation of $p(z\vert x)$, denoted $q^{* }_ {x(z)}$. Despite its probabilistic nature, we are looking for an encoding-decoding scheme as efficient as possible and, then, we want to choose the function $f$ that maximises the expected log-likelihood of $x$ given $z$ when $z$ is sampled from $q^{* }_ {x(z)}$.
In other words, for a given input $x$, we want to maximise the probability to have $\hat{x}= x$ when we sample $z$ from the distribution $q^{* }_ {x(z)}$ and then sample $\widehat{x}$ from the distribution $p(x\vert z)$.Thus, we are looking for the optimal $f^ {\star}$ such that –>
\[\begin{aligned} f^ {\star} &=\arg\max_ {f\in F}\,\mathbb{E}_ {z\sim q^ {\star}_ {x}}\left(\log p(x\vert z)\right)\\ &=\arg\max_ {f\in F}\,\mathbb{E}_ {z\sim q_{x}^ {\star}}\left(-\frac{\left\|x-f(z)\right\|^{2}}{2c}\right)\\ \end{aligned}\]ここで、$q^ {\star}_ {x(z)}$ は関数 $f$ に依存し,前述で求めたものである。 これらをまとめると,以下のような最適な $f^{\star}$, $g^ {\star}$, $h^ {\star}$ を探していることになる。
\(\left(f^{* },g^{* },h^{* }\right)=\arg\max_{(f,g,g)\in F\times G\times H}\left( \mathbb{E}_{z\sim q_{x}}\left(-\frac{\left\|x-f(z)\right\|^{2}}{2c}\right)-\text{KL}\left(q_{x}(z),p(z)\right) \right)\)
この目的関数には,前節の VAE の直感的な説明で紹介した要素を同定することができる。 $x$ と $f(z)$ の間の再構成誤差,$q_ {x}(z)$ と $p(z)$ (これは標準正規分布) の間の KL 発散で与えられる正則化項である。 また,前の 2 つの項の間のバランスを支配する定数 $c$ に注目することができる。 $c$ が高いほど,本モデルの確率的復号化の $f(z)$ の分散が大きいと仮定し,再構成項よりも正規化項を優先する ($c$ が低い場合はその逆となります)。
4.2 ニューラルネットワークをモデルへ取り込む
これまで $f$, $g$, $h$ の 3 つの関数に依存する確率モデルを設定し,変分推論を用いて $f^ {star}$ を得るために解くべき最適化問題を表現してきた。 このモデルで最適な符号化・復号化方式を与える $g^ {\star}$ と $h ^{\star}$ がある。 関数の空間全体を最適化することは容易ではないので,最適化領域を限定し $f$, $g$, $h$ をニューラルネットワークで表現することにした。 したがって $F$, $G$, $H$ はそれぞれネットワーク・アーキテクチャで定義される関数族に対応し,最適化はこれらのネットワークのパラメータに対して行われる。
実際には $g$ と $h$ は完全に独立した 2 つのネットワークで定義されるのではな く,そのアーキテクチャと重みの一部を共有しているので,以下のようになる。
\[\begin{aligned} g(x) &= g_{2}(g_{1})(x))\\ h(x) &= g_{2}(h_{1}(x))\\ g_{1}(x) &= h_{1}(x) \end{aligned}\]$q_{x(z)}$ の共分散行列を定義しているため,$h(x)$ は正方行列であることが前提となっている。 しかし,計算を簡略化し,パラメータ数を減らすために $p(z\vert x)$ の近似値である $q_{x}(z)$ が対角共分散行列を持つ多次元正規分布であるという仮定 (変数独立性の仮定) を追加する。 この仮定では $h(x)$ は単に共分散行列の対角要素のベクトルであり $g(x)$ と同じ大きさであることがわかる。 ただし,この方法では,変分推論で考慮する分布の族を減らすことになるので,得られる $p(z\vert x)$ の近似精度が低くなることがある。
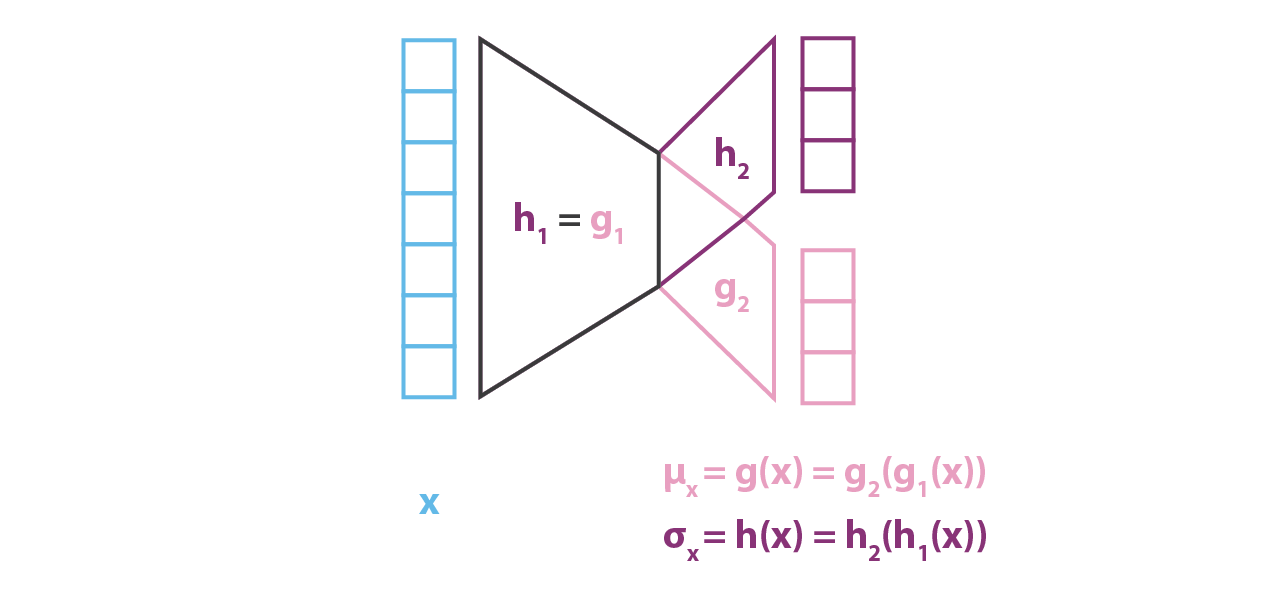
$p(z\vert x)$ をモデル化する符号化部では,平均と共分散が $x$ の関数であるガウス分布 ($g$ と $h$) を考えたのとは対照的に,本モデルでは $p(x\vert z)$ に共分散固定で正規分布を仮定している。 そのガウス分布の平均を定義する変数 $z$ の関数 $f$ をニューラルネットワークでモデル化し,次のように表現することができる。

そして,符号化器と復号化器の部分を連結することで,全体のアーキテクチャが出来上がる。 しかし,学習中に符号化器が返す分布からサンプリングする方法には,まだ十分な注意が必要である。 サンプリング処理は,誤差がネットワークを通じて逆伝播されるような方法で表現されなければならない。 これは,リパラメタタリゼーショントリック と呼ばれる簡単なトリックで,アーキテクチャの途中から発生するランダムなサンプリングにもかかわらず,勾配降下を可能にするために使用される。
\[z=h(x)\zeta + g(x)\hspace{1cm} \zeta\sim \mathcal{N}(0,I)\]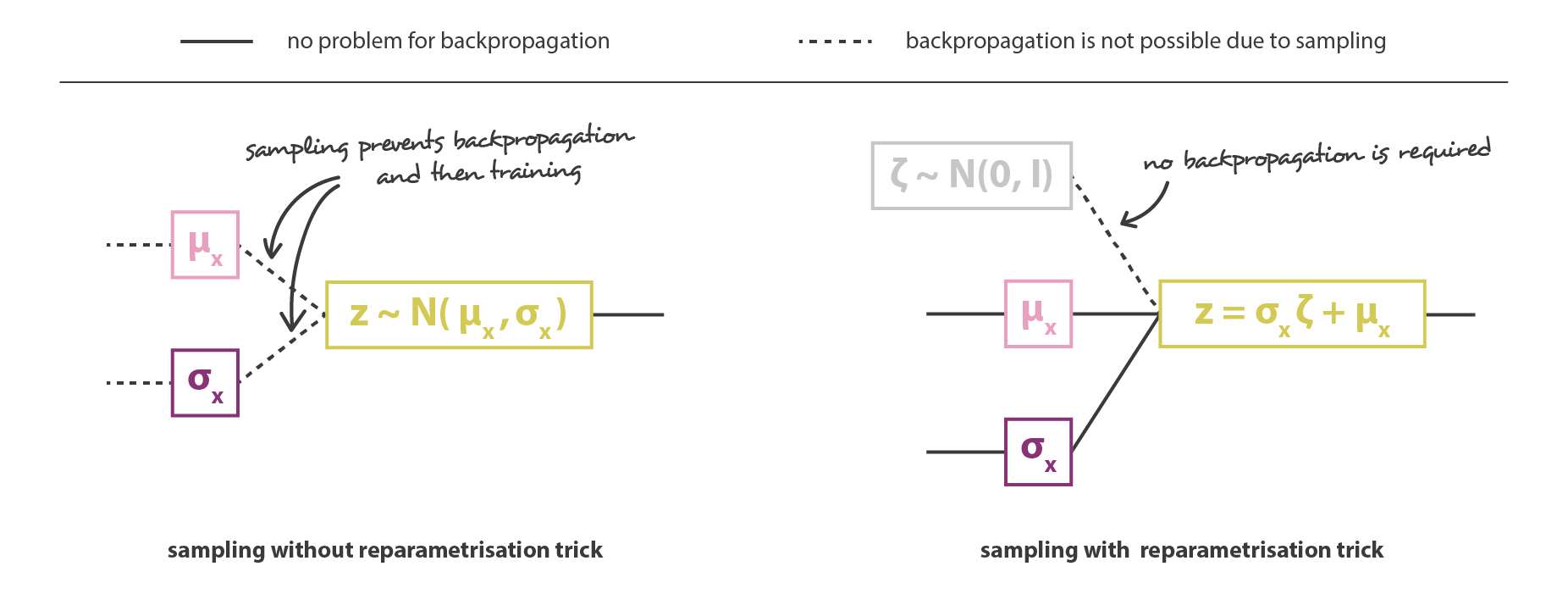
最後に,この方法で得られた変分自己符号化器アーキテクチャの目的関数は,理論的な期待値が,ほとんどの場合 1 回のドローで構成される多かれ少なかれ正確なモンテカルロ近似で置き換えられる前節の最後の式によって与えられる。 そこで,この近似を考慮し $C = 1/(2c)$ とすると,前節で直感的に導いた損失関数が復元され,再構成項,正則化項,およびこれら 2 項の相対重みを定義する定数で構成される。
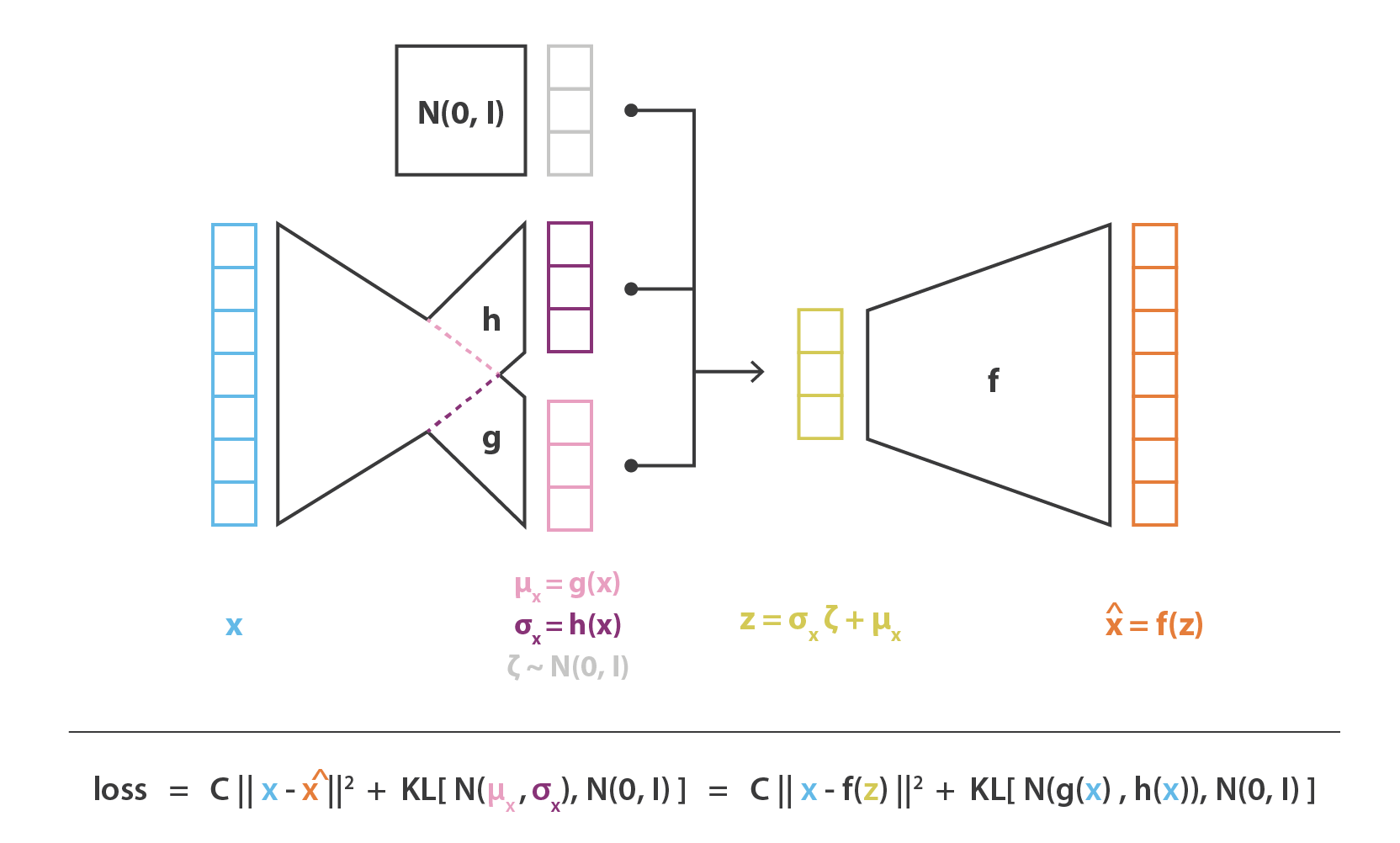
5. お持ち帰り
この記事の主な収穫は、以下の通り:
- 次元削減は,あるデータを記述する特徴の数を減らす処理である (初期の特徴のサブセットのみを選択するか,それらを組み合わせて新しい特徴を減らす)。したがって符号化の処理とみなすことができる。
- 自己符号化器は,符号化器と復号化器の両方で構成されるニューラルネットワークアーキテクチャで、データに対してボトルネックを作り,符号化-復号化処理で失う情報量を最小限にするように学習する (再構成エラーを減らす目的で勾配降下の繰り返しによって学習する)。
- オーバーフィッティングにより,自己符号化器の潜在空間は非常に不規則になることがある (潜在空間内の近い点は全く異なる復号化データを与える,潜在空間のいくつかの点は復号化されると無意味な内容を与える,など)。したがって,潜在空間から点を抽出し,復号化器を通過させて新しいデータを得るだけの生成処理は定義できない。
- 変分自己符号化器 (VAEs) は,潜在空間の不規則性の問題に取り組む自己符号化器で,符号化器が単一点の代わりに潜在空間上の分布を返すようにし,損失関数に潜在空間をよりよく構成するために,その返された分布の正則化項を追加します。
- データを記述するための単純な基本的確率モデルを仮定すると,再構成項と正則化項からなる VAE の非常に直感的な損失関数は,特に変分推論の統計的手法を使用して慎重に導き出すことができる (「変分」自己符号化器という名前もそのためである)。
結論として,ここ数年 GAN は VAE よりもはるかに多くの科学的貢献をしてきたと言える。 その理由として GAN の理論的基盤 (確率モデルや変分推論) が VAE の理論的基盤よりも複雑であること,そして GAN を支配する敵対的学習概念が単純であることが挙げられる。 今回の投稿では 今年の初めに GAN で行ったように,VAE を初めて使う人にも分かりやすくするために,価値ある直観と強力な理論的基盤を共有できたのではないかと思っている。 しかし,両者を深く議論した今,一つの疑問が残る。あなたは GAN と VAE,どちらが好きですか?
読んでくれてありがとう